| Student | イチゴ | オレンジ | スモモ | ハッカ | パイン | メロン | リンゴ | レモン |
|---|---|---|---|---|---|---|---|---|
| A | 4 | 3 | 8 | 2 | 4 | 10 | 5 | 5 |
| B | 8 | 6 | 5 | 3 | 4 | 3 | 3 | 3 |
| C | 8 | 5 | 7 | 3 | 4 | 8 | 5 | 6 |
| D | 8 | 6 | 4 | 3 | 7 | 6 | 5 | 5 |
| E | 5 | 8 | 4 | 3 | 3 | 6 | 8 | 4 |
データの可視化と記述統計量
サクマドロップス
2024 / 07 / 07
サクマドロップスのサンプル表
一回目の講義には、キャンバスバッグからサクマドロップスを採取しました。 キャンバスバッグにあるサクマドロップスの種類ごと数を知ることが目的です。 本来知りたい集団全体のことを母集団 (population)とよび、母集団から採取したデータは標本 (sample)といいます。
学生ごとに一度だけ標本をとったので、表には5つの標本を示している。
標本から母数団の情報を推定するので、標本の代表的な値を求めます。
データを代表する値
平均値 (mean, average): 総和を標本数で割った値
\[ \bar{x} = \frac{1}{N} \sum_{n=1}^{N} x_n \]
中央値 (median): 標本を上順に並べたときに、データの中央に位置する値
\[ M = \cases{ x_{[\frac{1}{2}(N + 1)]} & $N$ が奇数 \\ \frac{1}{2}\left(x_{[\frac{N}{2}]} + x_{[\frac{N}{2} + 1]}\right) & $N$ が偶数 } \]
最頻値 (mode): 標本で最も頻繁に現れる値
平均値の求め方
オレンジサクマドロップスのサンプルをまとめます。
\[ \bar{x} = \frac{1}{5} (3 + 6 + 5 + 6 + 8) = 5.6 \]
中央値の求め方
オレンジサクマドロップスの中央値を求めるなら、サンプルを上順に並べる必要があります。
\[ (3, 5, 6, 6, 8) \]
\(n = 5\) なので、中央値は、
\[ x_{[\frac{1}{2}(5 + 1)]} = x_{[3]} = 6 \]
サクマドロップスの統計量
全種類のサクマドロップスの平均値、中央値、最頻値を求めます。 少量のデータなら、表でまとめることもあるが、データ数が増えると図のほうが見やすい。
| Student | イチゴ | オレンジ | スモモ | ハッカ | パイン | メロン | リンゴ | レモン |
|---|---|---|---|---|---|---|---|---|
| A | 4.0 | 3.0 | 8.0 | 2.0 | 4.0 | 10.0 | 5.0 | 5.0 |
| B | 8.0 | 6.0 | 5.0 | 3.0 | 4.0 | 3.0 | 3.0 | 3.0 |
| C | 8.0 | 5.0 | 7.0 | 3.0 | 4.0 | 8.0 | 5.0 | 6.0 |
| D | 8.0 | 6.0 | 4.0 | 3.0 | 7.0 | 6.0 | 5.0 | 5.0 |
| E | 5.0 | 8.0 | 4.0 | 3.0 | 3.0 | 6.0 | 8.0 | 4.0 |
| Mean | 6.6 | 5.6 | 5.6 | 2.8 | 4.4 | 6.6 | 5.2 | 4.6 |
| Median | 8.0 | 6.0 | 5.0 | 3.0 | 4.0 | 6.0 | 5.0 | 5.0 |
| Mode | 8.0 | 6.0 | 4.0 | 3.0 | 4.0 | 6.0 | 5.0 | 5.0 |
棒グラフ
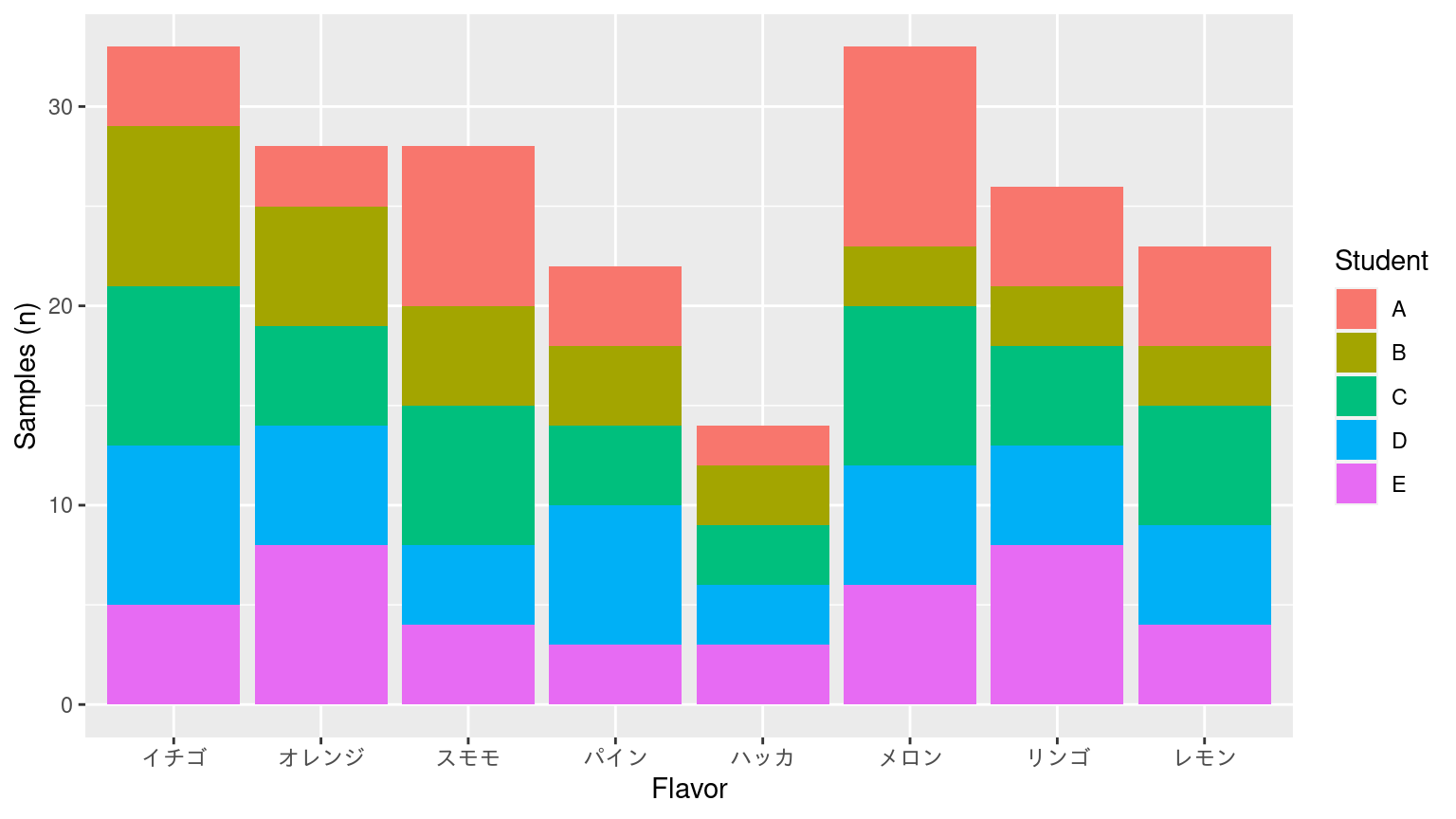
Stacked bar chart
棒グラフ
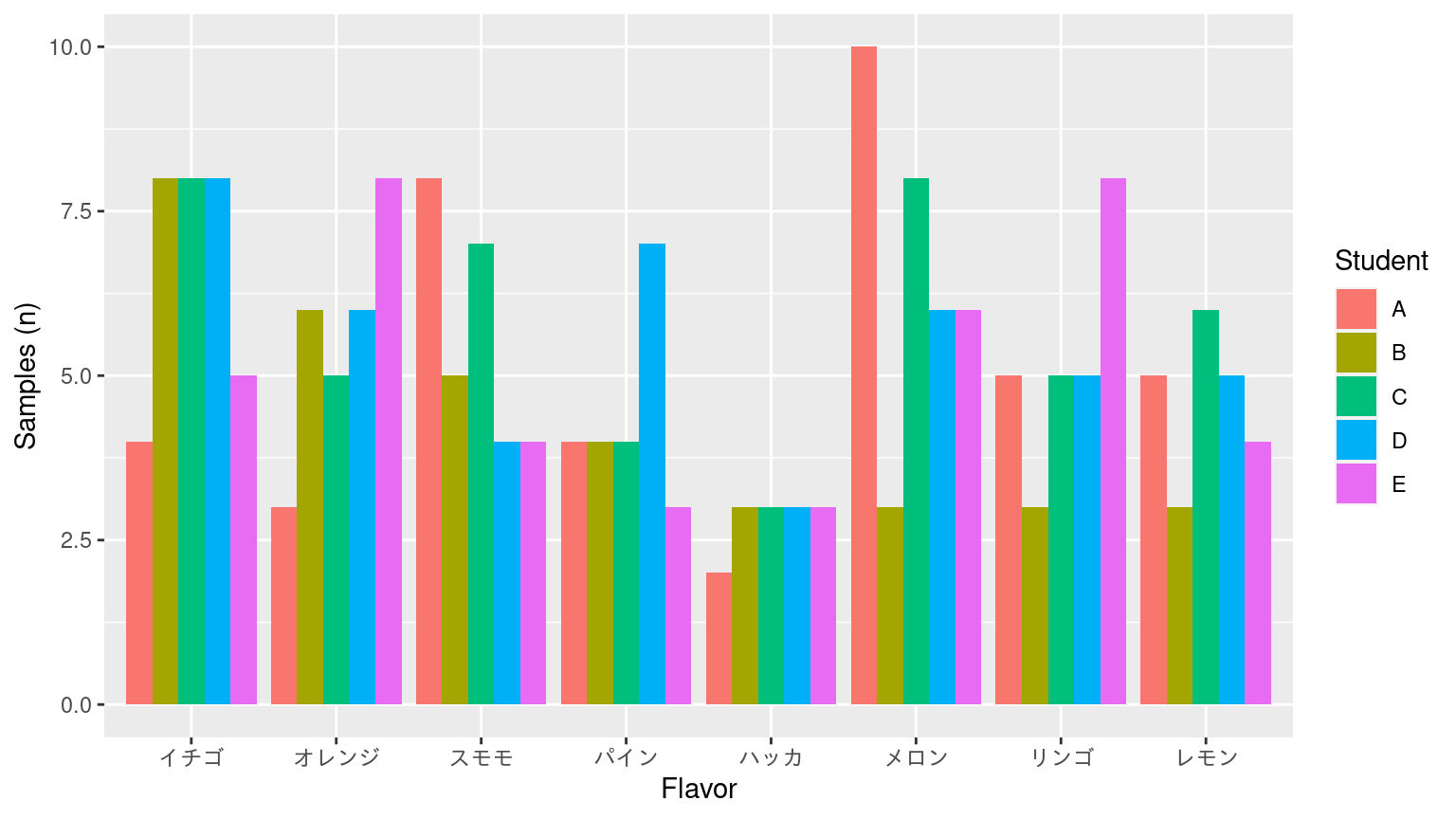
Grouped bar chart
散布図
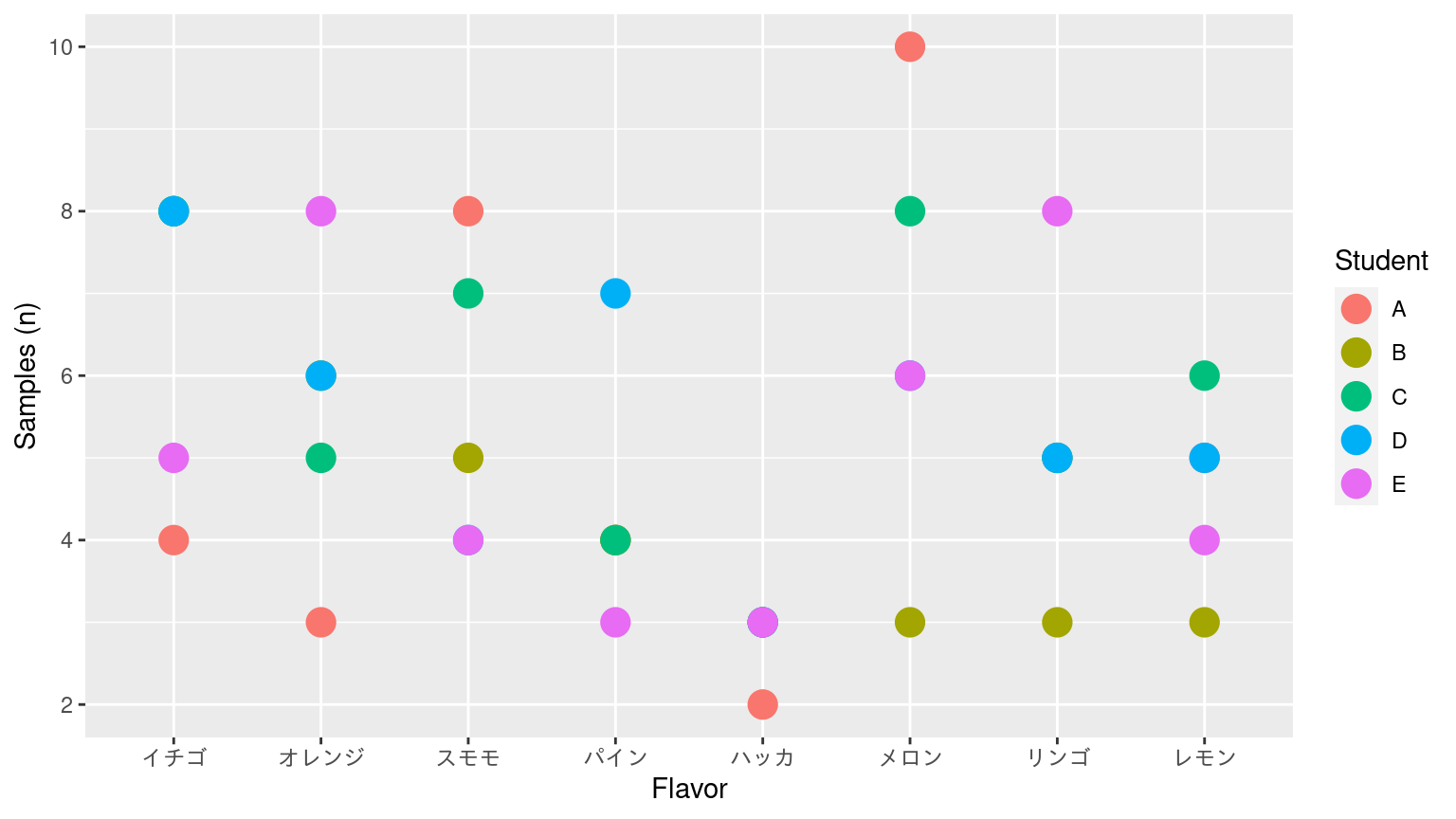
Scatter plot
散布図
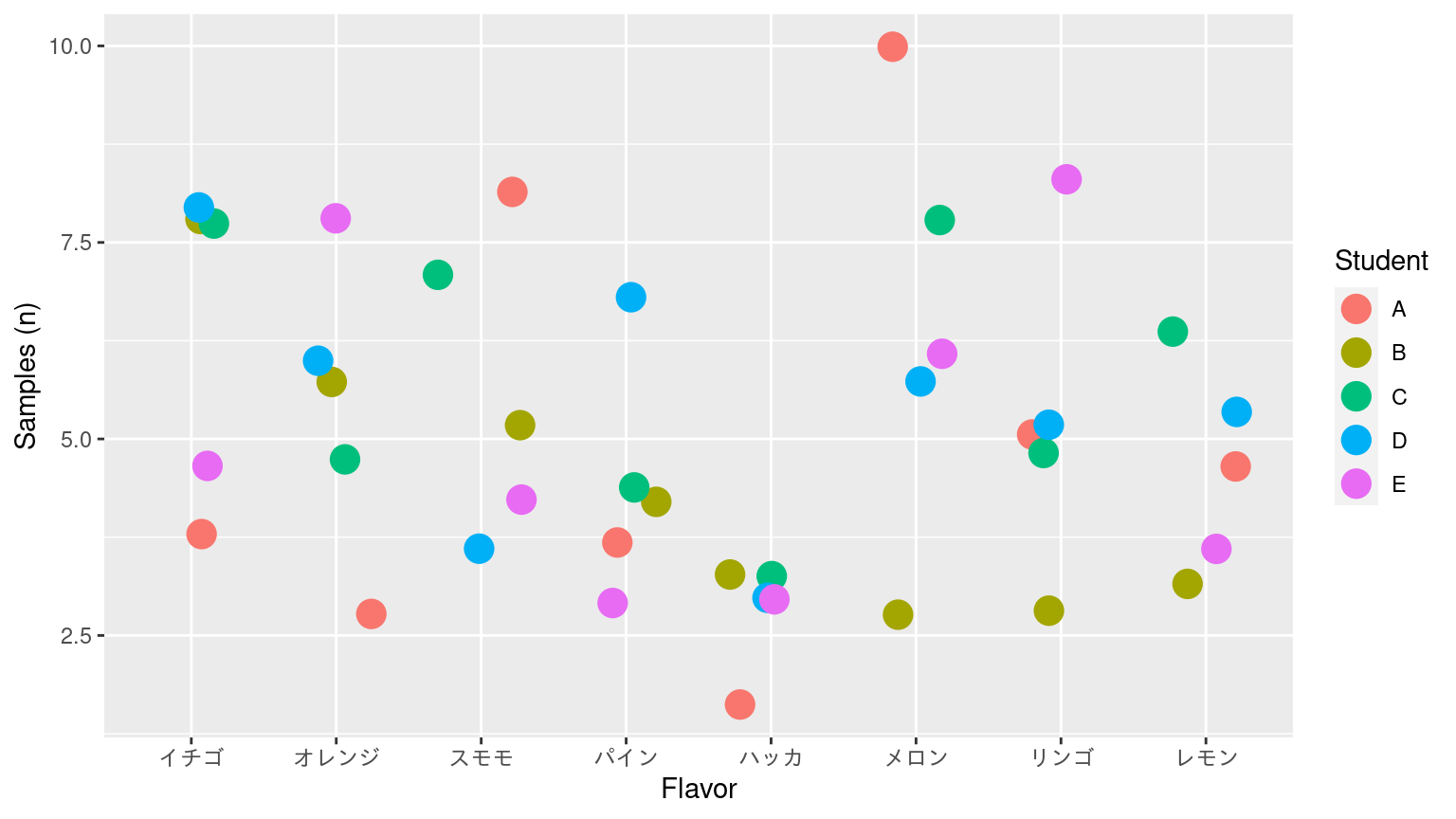
Jittered scatter plot
箱ひげ図
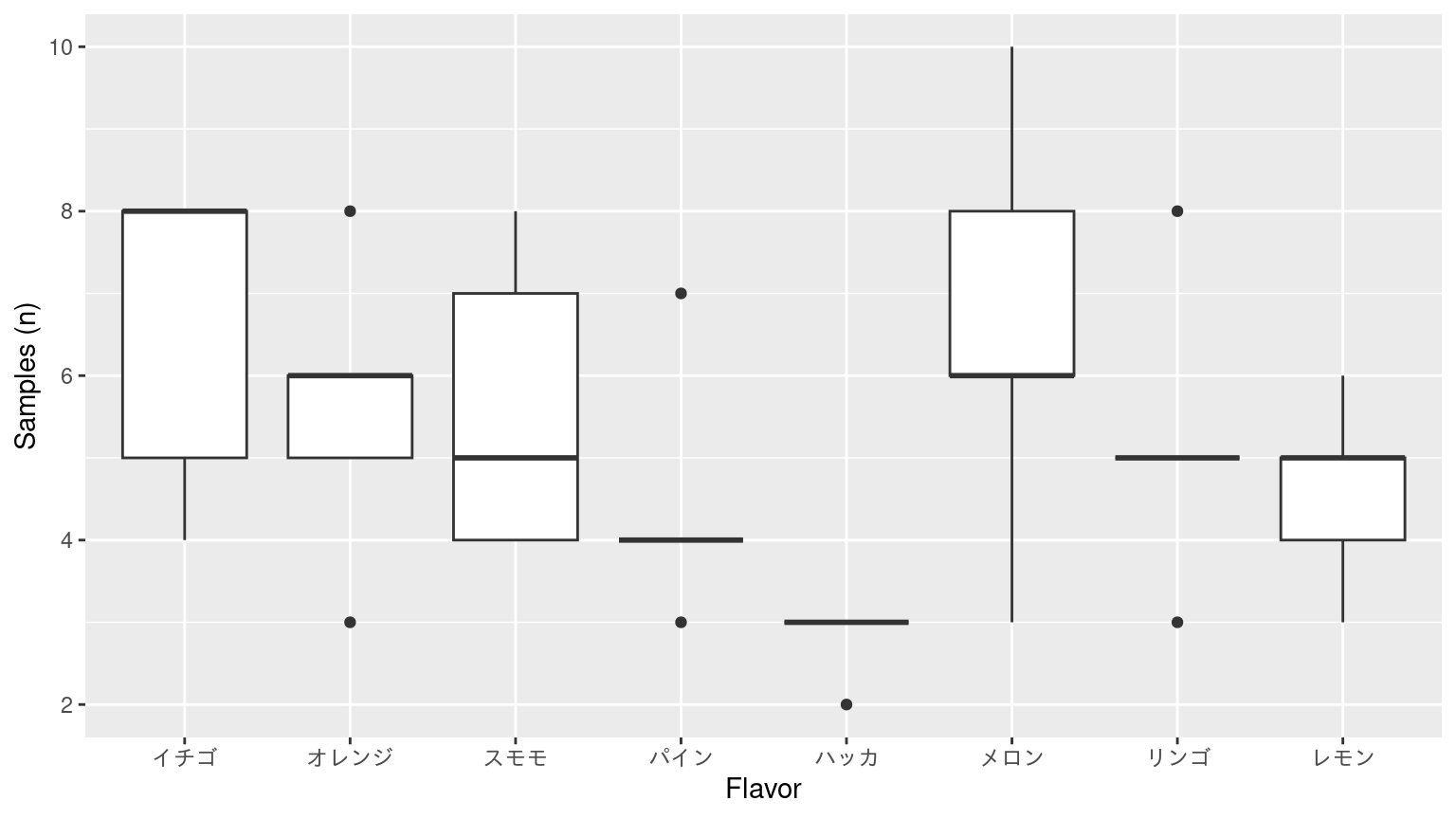
Box-and-whisker plot
箱ひげ図について
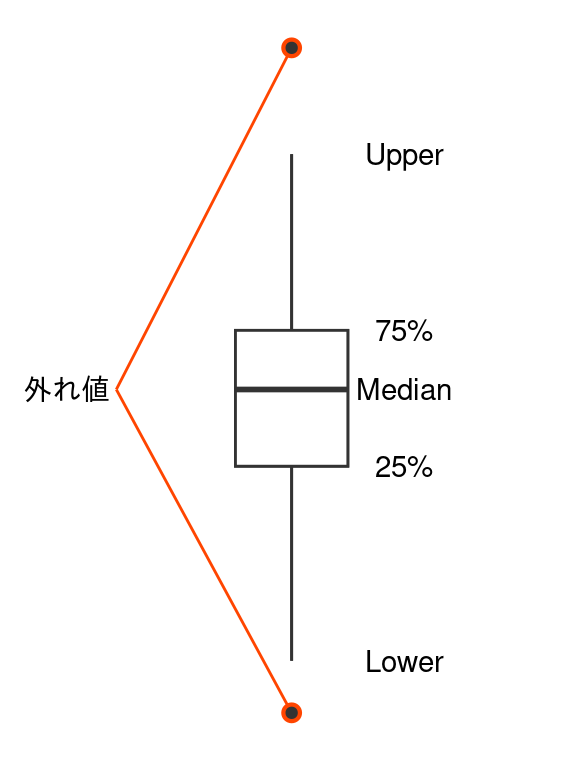
- Median: 中央値または第2分位点
- 箱の上下の辺は第1 (25%) と第3四分位点 (75%)を示す。50%のサンプルは箱内にある。
- 上下のヒゲ (Upper & Lower) は、それぞれの四分位点の位置から、極値までの間を示す。 極値とは、第1または第3四分位点から箱の高さの 1.5 倍以内にあるサンプルのうちの最大値と最小値です。
- ひげの範囲外のサンプルは点として示される。
データの可視化の重要なポイント
- 複雑なデータの関係を明確に、簡潔に、雑味のないように示す
- 相手に重要なポイントをすぐに把握できるように示す
- 適切な視覚的要素を用いて、データに含まれる情報やアイデアを効果的に伝える
- フォント、フォントサイズ、色、記号の種類を相手にあわせる
- 読みやすいフォントを選ぶ
- 色覚異常を意識すること
- シンプルでわかりやすい図を作図する・不必要な要素をいれない。
- 信頼できる正確な、最新なデータを用いる
区別しづらい色の組み合わせ

参考:(https://www.morisawa.co.jp/blogs/MVP/5369)
サンプル数の総和で表す
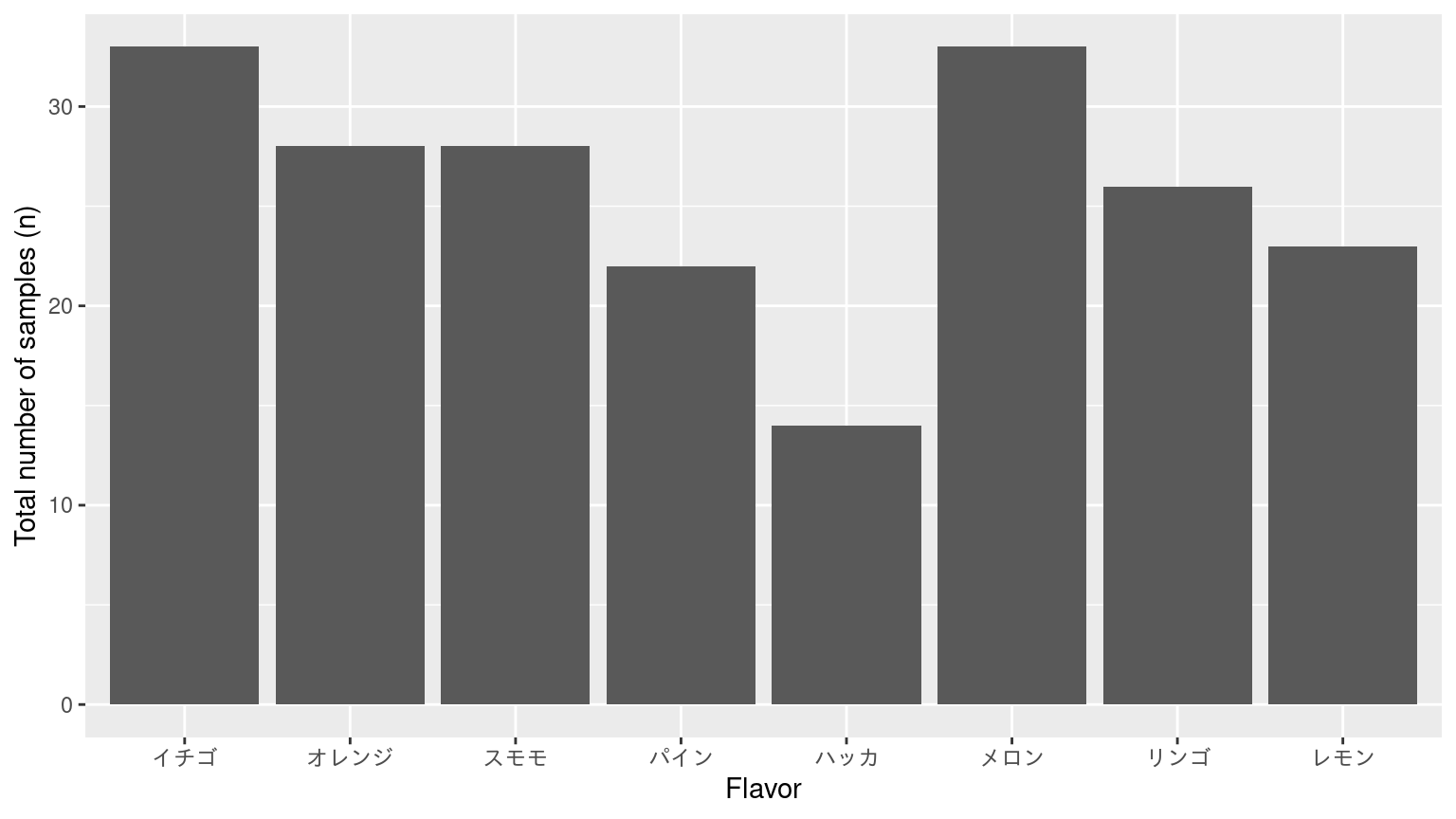
サンプル数の総和で表す
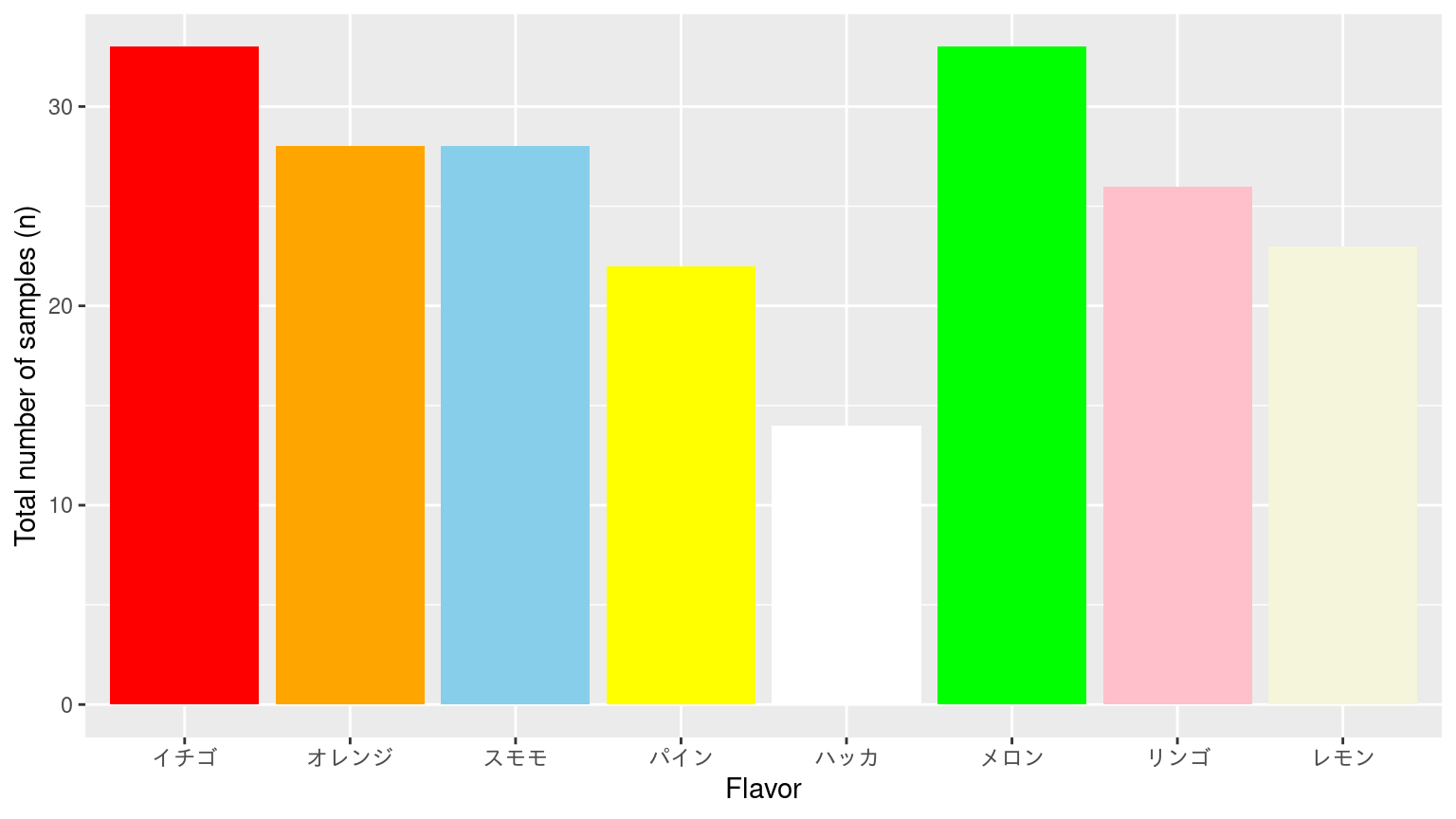
色を加えるなら、資料と合わせる。
サンプル数の総和で表す
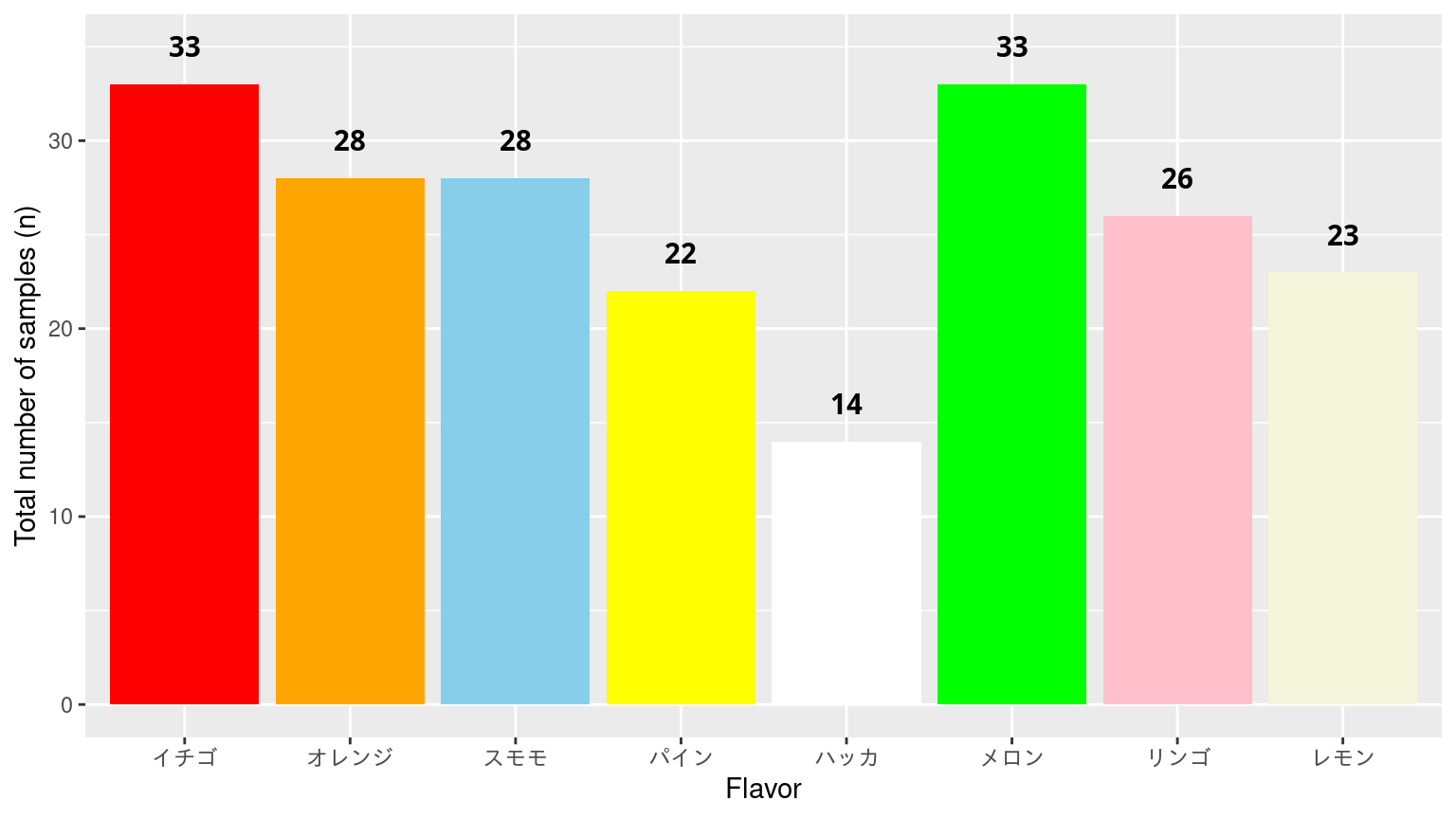
場合によって、図に数値情報も加えるといい。ここでは、棒の上に総数を追加した。
平均値で表す

学生が採取したサンプルの学生ごとの合計は異なる。 5回分の情報を総数で示すのはあまりよろしくない。Why?
平均値で表す
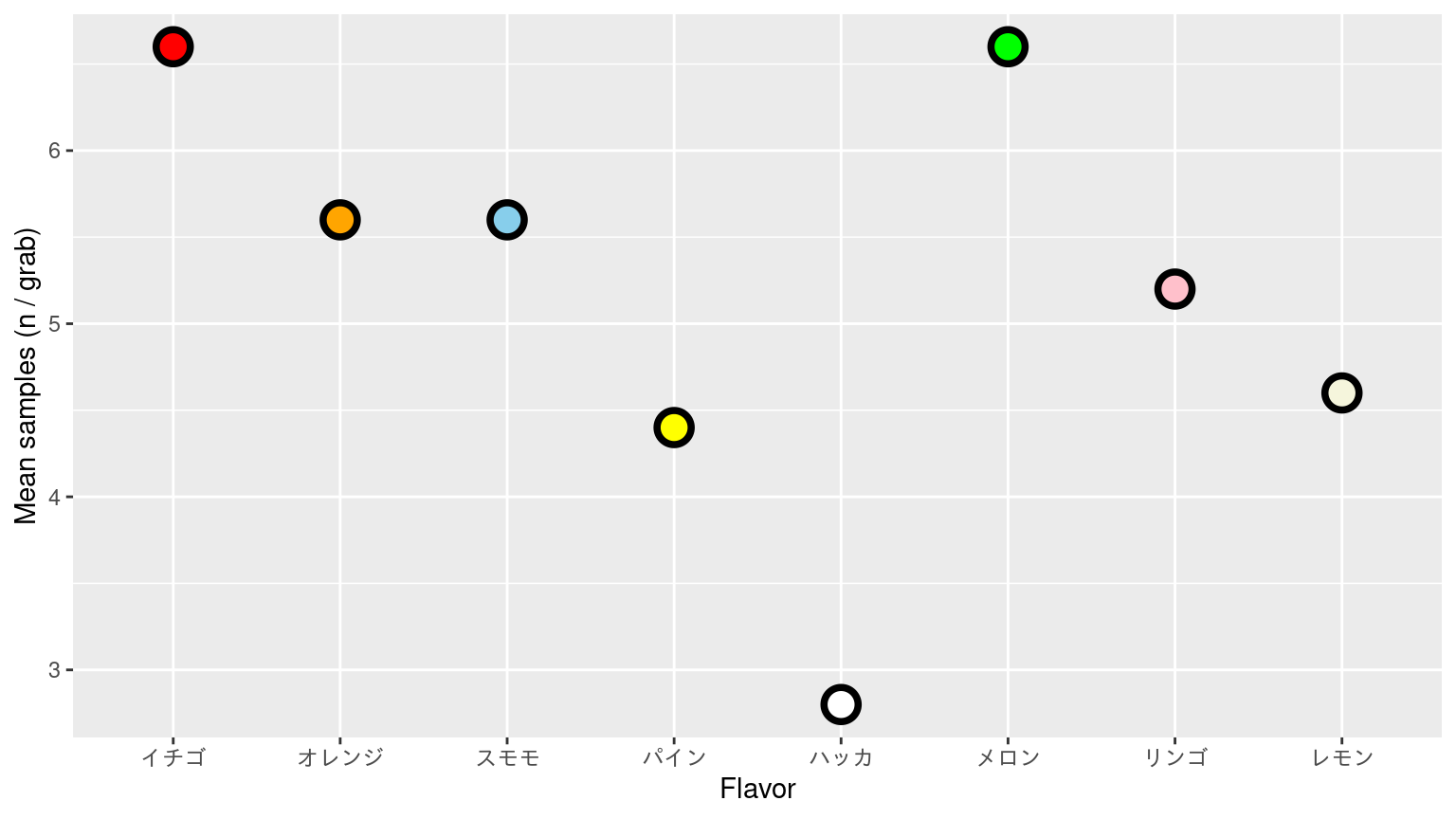
データの分布

データの見せ方
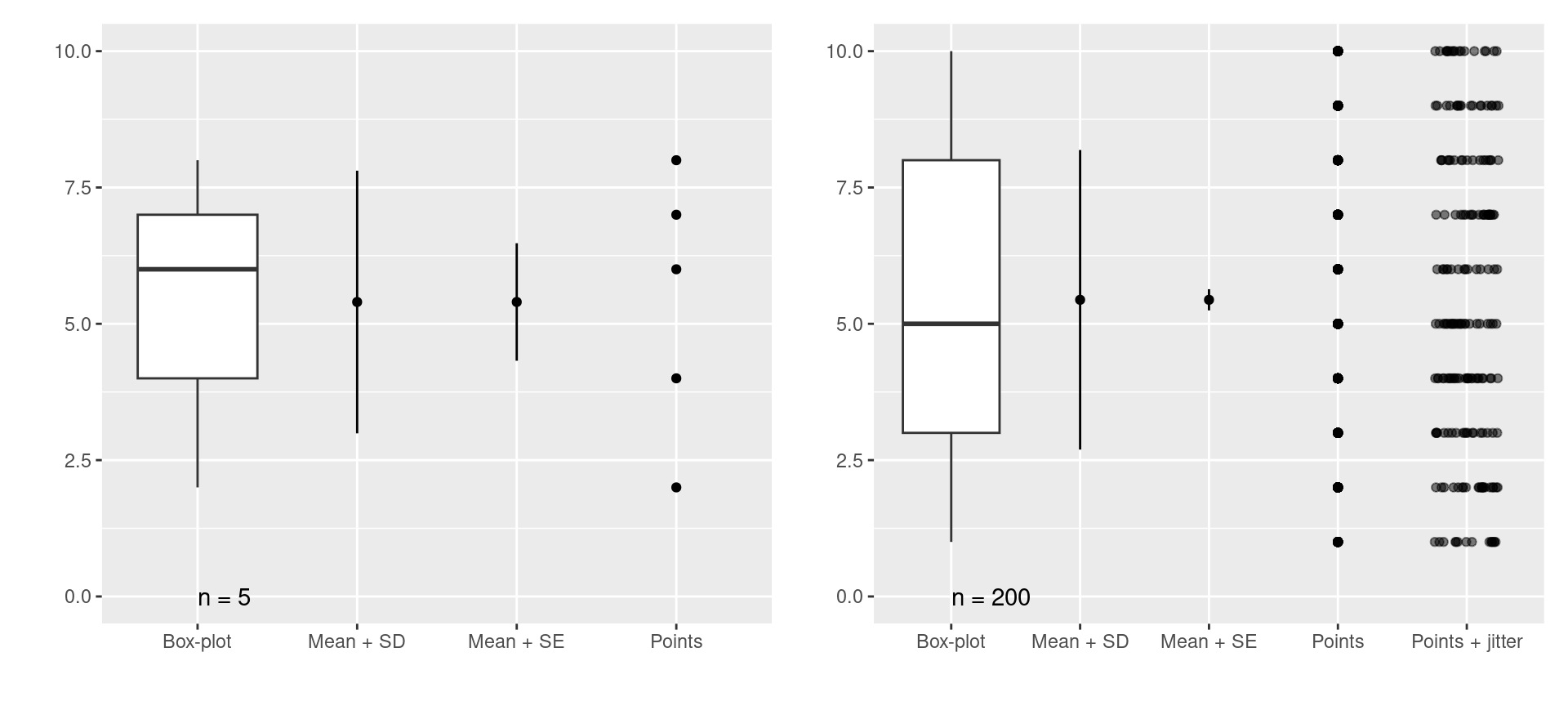
図はサンプル数に合わせて、見せ方を工夫する。
データのばらつき
標準偏差 (standard deviation):
\[ s = \sqrt{\frac{1}{N-1} \sum_{n=1}^N\left(x - \bar{x}\right)^2} \]
\(x - \bar{x}\) は残渣と呼ぶ。
平均絶対偏差 (mean absolute deviation) & 中央絶対残渣 (median absolute deviation)
\[ \text{MAD} = \frac{1}{N} \sum_{n = 1}^{N} |x - m(x)| \]
\[ \text{MAD} = median(|x - \tilde{x}|) \] \(m(x)\) は平均値または中央値、\(\tilde{x}\) は中央値。一般的には MAD が諸略なので、何が計算されたのかをよく調べること。
標準偏差の求め方
\[ \bar{x} = 5.6 \]
\[ s = \sqrt{\frac{1}{5-1} (3-5.6)^2 + (6-5.6)^2 + (5-5.6)^2 + (6-5.6)^2 + (8-5.6)^2} \] \[ s = 1.8165902 \]
標準偏差付き散布図
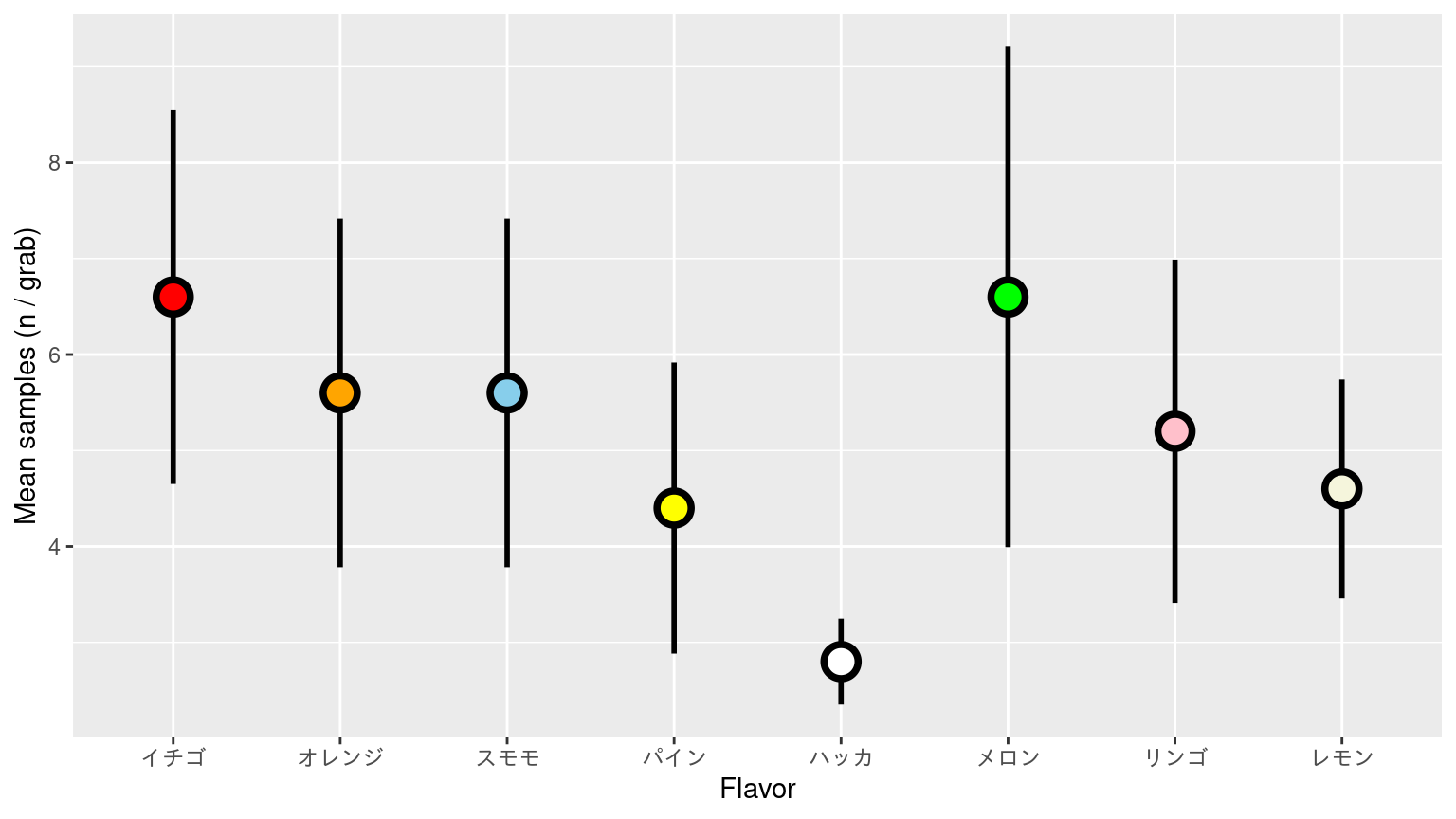
平均の制度
\[ \text{S.E.} = \frac{s}{N} \]
\(s\) は標準偏差、\(\text{S.E.}\) は Standard Error の諸略(標準誤差)。
標準誤差の求め方
\[ \bar{x} = 5.6 \]
\[ \text{S.E.} = \frac{1}{5}\sqrt{\frac{1}{5-1} (3-5.6)^2 + (6-5.6)^2 + (5-5.6)^2 + (6-5.6)^2 + (8-5.6)^2} \] \[ \text{S.E.} = 0.363318 \]
標準誤差付き散布図
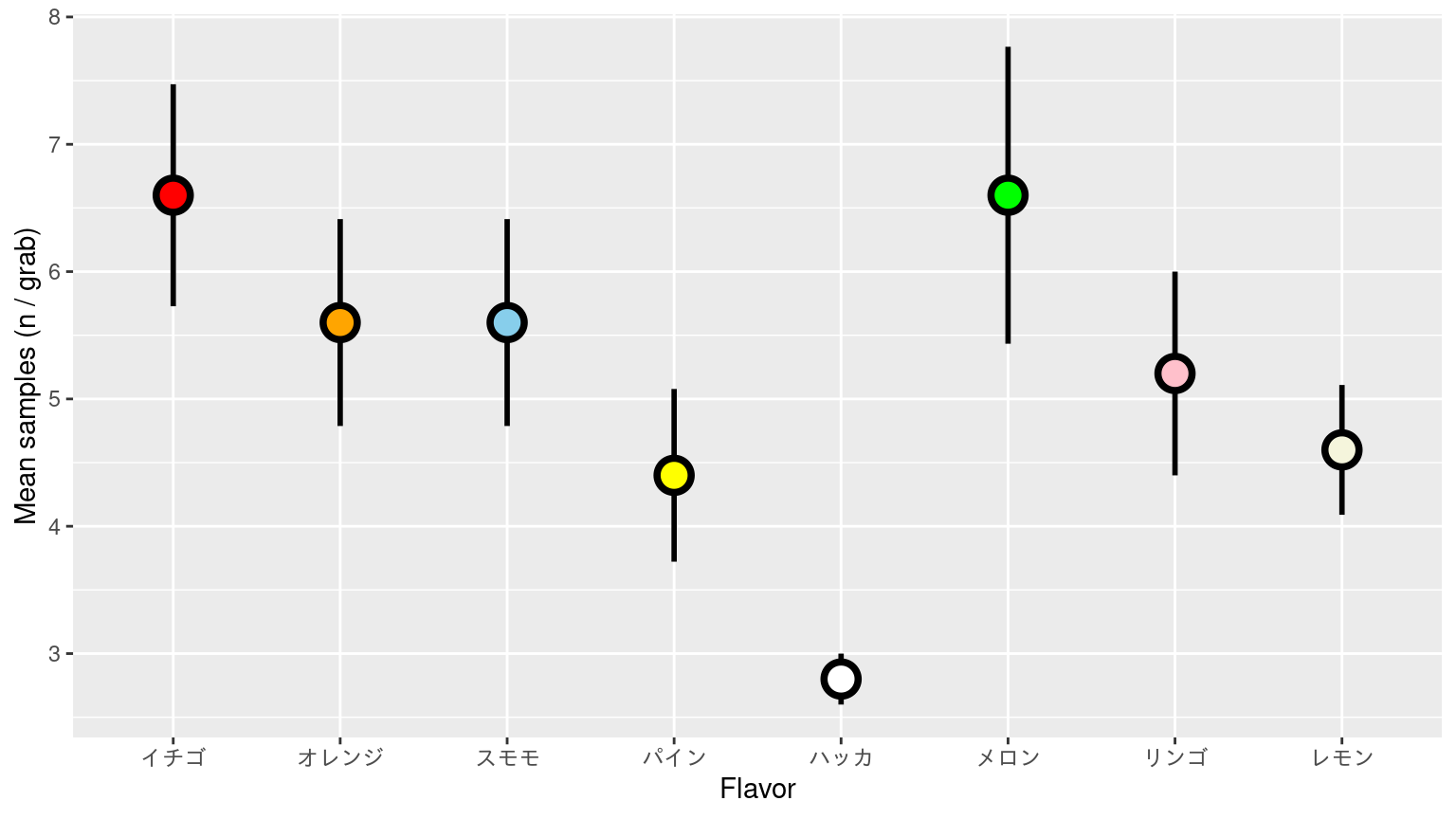
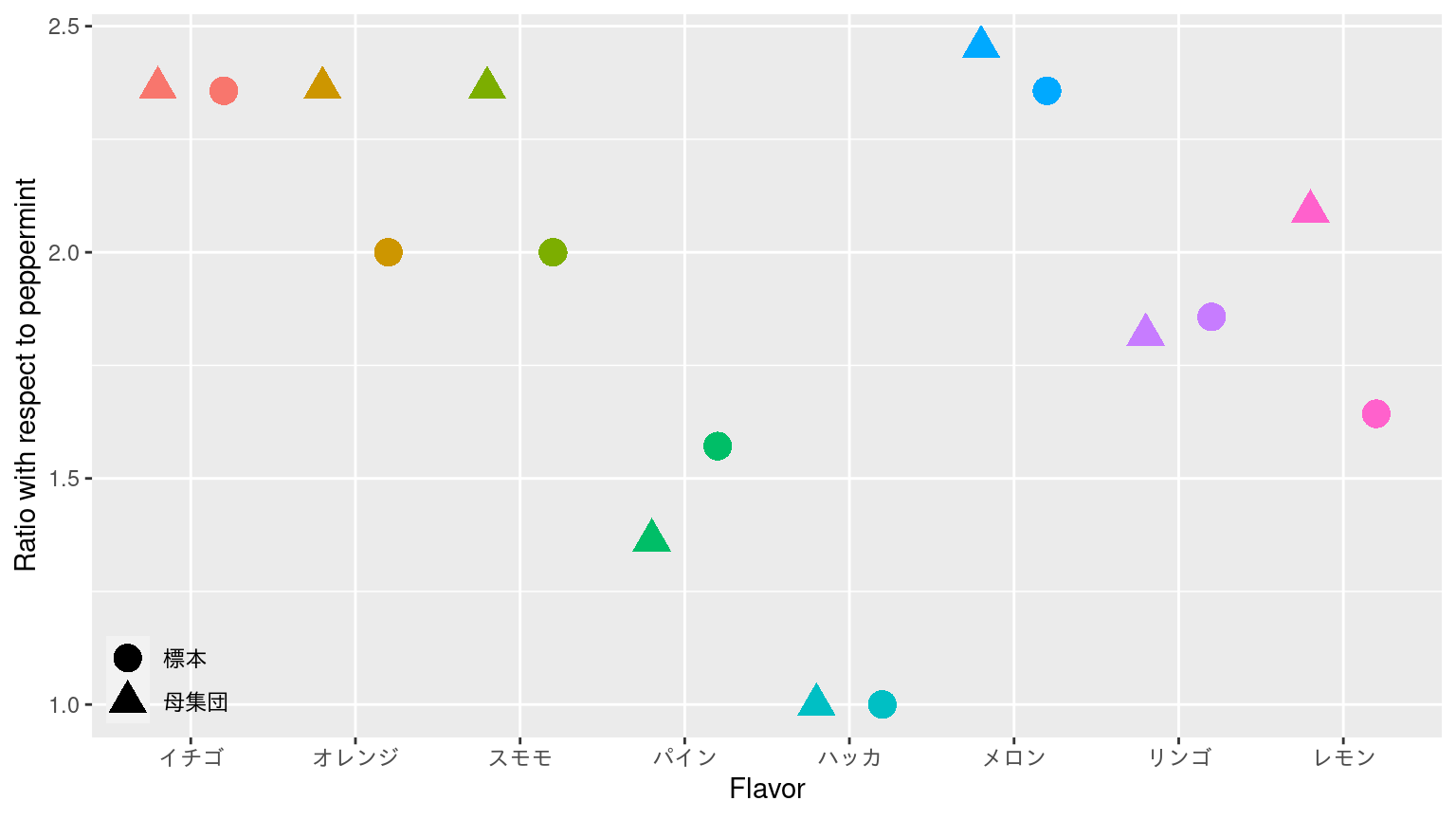
母集団と平均値の比較
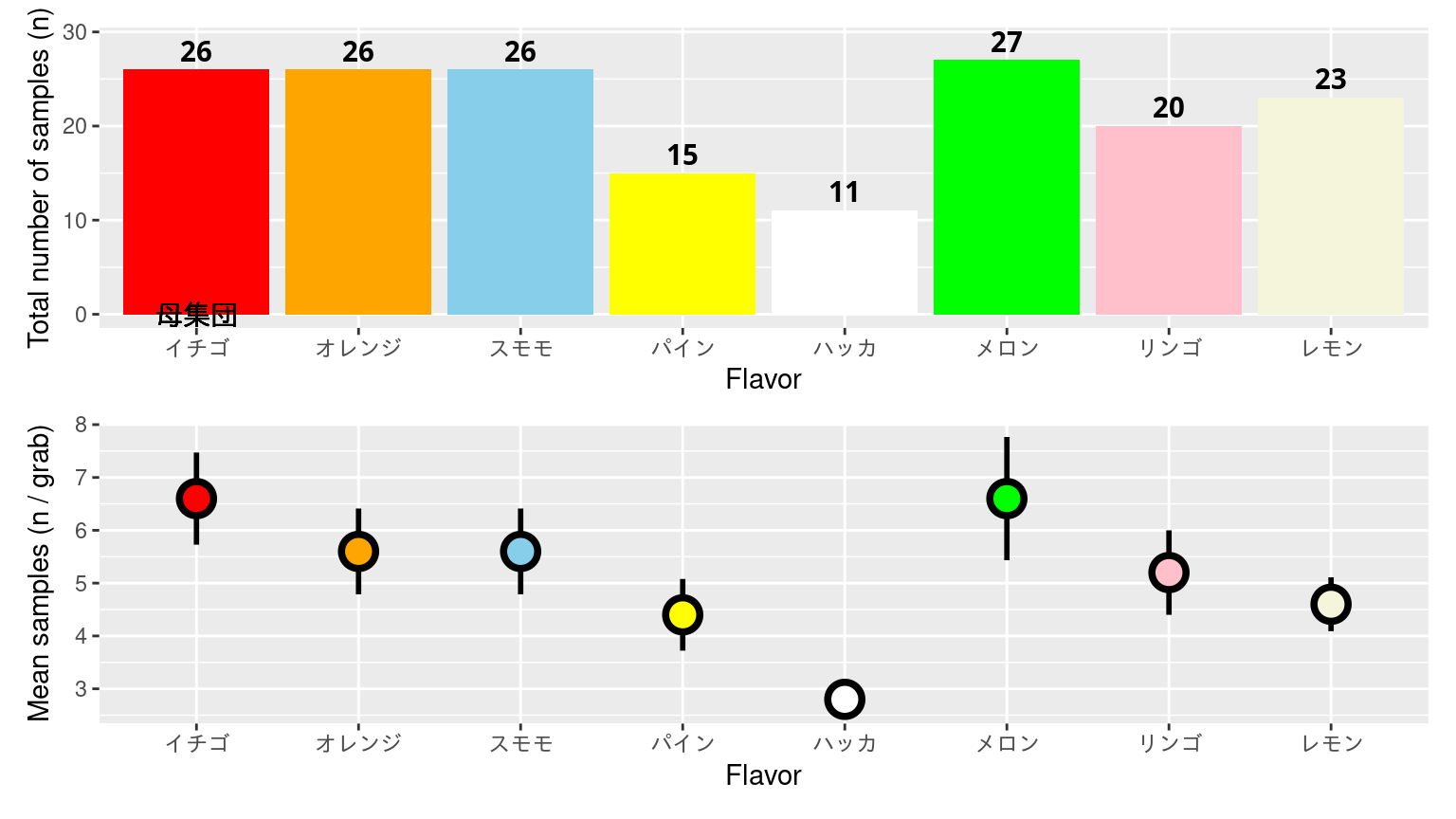
割合の比較