7 分散分析
7.2 データの読み込み
rootdatafolder = rprojroot::find_rstudio_root_file("Data/")
filename = '瀬戸内海藻場データ.xlsx'
path = str_c(rootdatafolder, filename)
# fy1990 の処理
RNG = "A4:C27" # セルの範囲
SHEET = "FY1990" # シート名
d19 = read_xlsx(path, sheet = SHEET, range = RNG)
d19 = d19 |>
rename(site = 調査海域, seaweed = 海藻, seagrass = 海草) |>
mutate(site = factor(site, levels = c('東部', '中部', '西部')))
# fy2018の処理
RNG = "A6:C15" # 海藻データのセル範囲
SHEET = "FY2018" # シート名
seaweed = read_xlsx(path, sheet = SHEET, range = RNG)
RNG = "E6:G15" # 海草データのセル範囲
seagrass = read_xlsx(path, sheet = SHEET, range = RNG)
seaweed = seaweed |> pivot_longer(cols = everything())
seagrass = seagrass |> pivot_longer(cols = everything())
d20 = bind_rows(seaweed = seaweed, seagrass = seagrass, .id = "type")
d20 = d20 |> pivot_wider(id_cols = name,
names_from = type, values_from = value,
values_fn = "list")
d20 = d20 |> unnest(c(seaweed, seagrass)) |> rename(site = name) |> drop_na()
d20 = d20 |>
mutate(site = factor(site, levels = c('東部', '中部', '西部')))7.3 一元配置分散分析
では、一元配置分散分析を実施します。
まず、分散分析の平方和を正しく求めるためには、contr.sum を設定することです。
その処理のあと、lm() 関数でモデルを当てはめます。
lm() 関数に渡すモデルは、 〜 の右辺に説明変数、左辺に観測値を指定しましょう。
contrasts(d19$site) = contr.sum
contrasts(d20$site) = contr.sum
m19 = lm(seaweed ~ site, data = d19)
m20 = lm(seaweed ~ site, data = d20)FY1990 海藻藻場面積の一元配置分散分析の結果は次のとおりです。
anova(m19) # FY1990 の処理
#> Analysis of Variance Table
#>
#> Response: seaweed
#> Df Sum Sq Mean Sq F value Pr(>F)
#> site 2 892963 446482 2.6621 0.09439 .
#> Residuals 20 3354343 167717
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1FY2019 海藻藻場面積の一元配置分散分析の結果は次のとおりです。
anova(m20) # FY2018 の処理
#> Analysis of Variance Table
#>
#> Response: seaweed
#> Df Sum Sq Mean Sq F value Pr(>F)
#> site 2 330811 165405 2.9569 0.07499 .
#> Residuals 20 1118771 55939
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1FY1990 のP値は P = 0.0944、 FY2018 のP値は P = 0.0750 でした。 どちらも有意水準 (α = 0.05) より大きいので、帰無仮説(海域間の藻場面積は同じ)を棄却できません。
等分散性と正規性の検定を無視したように、今回だけ分散分析の結果を無視して、多重比較をしてみます。
7.4 多重比較
調査海域の全ペアの比較をしるので、Tukey HSDを用います。
e19 = emmeans(m19, specs = pairwise ~ site, adjust = "tukey")
e20 = emmeans(m20, specs = pairwise ~ site, adjust = "tukey")FY2019 の場合、全ペアを比較したら、有意な結果はありません。
e19 # FY1990 の処理
#> $emmeans
#> site emmean SE df lower.CL upper.CL
#> 東部 118 167 20 -230 467
#> 中部 205 137 20 -80 490
#> 西部 578 145 20 276 880
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> 東部 - 中部 -86.4 216 20 -0.400 0.9158
#> 東部 - 西部 -459.3 221 20 -2.077 0.1202
#> 中部 - 西部 -372.8 199 20 -1.874 0.1723
#>
#> P value adjustment: tukey method for comparing a family of 3 estimatesFY2020 も同じですね。
e20 # FY2018 の処理
#> $emmeans
#> site emmean SE df lower.CL upper.CL
#> 東部 109.3 96.6 20 -92.1 311
#> 中部 301.0 78.8 20 136.5 465
#> 西部 29.2 83.6 20 -145.2 204
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> 東部 - 中部 -191.7 125 20 -1.538 0.2953
#> 東部 - 西部 80.1 128 20 0.627 0.8072
#> 中部 - 西部 271.8 115 20 2.365 0.0696
#>
#> P value adjustment: tukey method for comparing a family of 3 estimatesこの用な結果は予想していました。そもそも分散分析から有意な結果がでなかったので、多重比較しても有意な結果はでません。
ちなみに Dunnet Method をつかって、西部と東部を中部と比較したら次の結果になります。
e19d = emmeans(m19, specs = trt.vs.ctrl ~ site, ref = 2)
e20d = emmeans(m20, specs = trt.vs.ctrl ~ site, ref = 2)
e19d # FY1990 の処理
#> $emmeans
#> site emmean SE df lower.CL upper.CL
#> 東部 118 167 20 -230 467
#> 中部 205 137 20 -80 490
#> 西部 578 145 20 276 880
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> 東部 - 中部 -86.4 216 20 -0.400 0.8781
#> 西部 - 中部 372.8 199 20 1.874 0.1373
#>
#> P value adjustment: dunnettx method for 2 tests
e20d # FY2018 の処理
#> $emmeans
#> site emmean SE df lower.CL upper.CL
#> 東部 109.3 96.6 20 -92.1 311
#> 中部 301.0 78.8 20 136.5 465
#> 西部 29.2 83.6 20 -145.2 204
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> 東部 - 中部 -192 125 20 -1.538 0.2441
#> 西部 - 中部 -272 115 20 -2.365 0.0531
#>
#> P value adjustment: dunnettx method for 2 testsDunnet Method の場合でも有意な結果はありません。
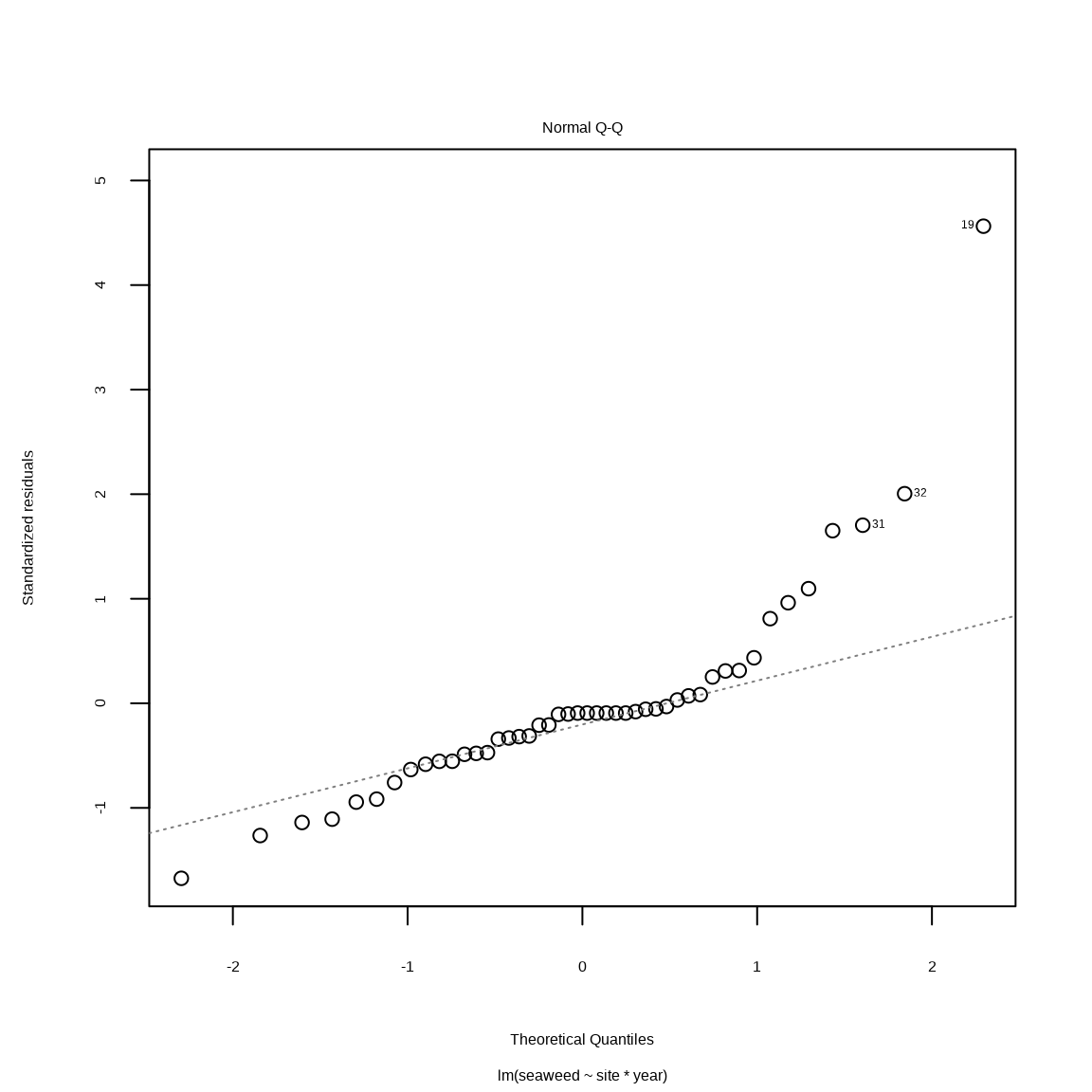
7.6 正規性と等分散性の確認
dall = bind_rows(fy1990 = d19,
fy2018 = d20,
.id = "year")
dall = dall |> mutate(year = factor(year))分散分析を行う前に、Levene Test と Shapiro-Wilk Normality Test でデータの等分散性9 と正規性10 を確認します。
ルビーン検定とシャピロウィルク検定については、t 検定の資料を参考にしてください。
ここで紹介する解析は 海藻 に対してです。
ルビーン検定
FY1990とFY2018 データの等分散性検定結果は P = 0.0996 でしたので、
帰無仮説は棄却できません。
つまり、等分散性であると判断できます。
leveneTest(seaweed ~ site*year, data = dall)
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 5 1.9994 0.0996 .
#> 40
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1シャピロウィルク検定
FY1990とFY2018 データの等分散性について、P < 0.0001 だったので、
帰無仮説を棄却できます。
データの母集団は正規分布に従わないかもしれないです。
shapiro.test(x = dall$seaweed) # FY1990 の処理
#>
#> Shapiro-Wilk normality test
#>
#> data: dall$seaweed
#> W = 0.63263, p-value = 1.731e-097.7 二元配置分散分析
では、二元配置分散分析を実施します。
まず、分散分析の平方和を正しく求めるためには、contr.sum を設定することです。
その処理のあと、lm() 関数でモデルを当てはめます。
lm() 関数に渡すモデルは、 〜 の右辺に説明変数、左辺に観測値を指定しましょう。
contrasts(dall$site) = contr.sum
contrasts(dall$year) = contr.sum
mall = lm(seaweed ~ site*year, data = dall)FY1990 海藻藻場面積の一元配置分散分析の結果は次のとおりです。
Anova(mall, type =3)
#> Anova Table (Type III tests)
#>
#> Response: seaweed
#> Sum Sq Df F value Pr(>F)
#> (Intercept) 2230084 1 19.9421 6.382e-05 ***
#> site 256846 2 1.1484 0.32738
#> year 263994 1 2.3607 0.13230
#> site:year 966928 2 4.3233 0.01996 *
#> Residuals 4473114 40
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1site 効果のP値は P = 0.3274、
year 効果のP値は P = 0.1323、
相互作用のP値は P = 0.0200 でした。
相互作用のP値は有意水準 (α = 0.05) より大きいので、相互作用の帰無仮説は棄却できますが、主効果の帰無仮説は棄却できません。
7.8 多重比較
調査海域の全ペアの比較をしるので、Tukey HSDを用います。
eall = emmeans(mall, specs = pairwise ~ site:year, adjust = "tukey")FY2019 の場合、全ペアを比較したら、有意な結果はありません。
eall
#> $emmeans
#> site year emmean SE df lower.CL upper.CL
#> 東部 fy1990 118.3 137 40 -157.6 394
#> 中部 fy1990 204.8 111 40 -20.5 430
#> 西部 fy1990 577.6 118 40 338.7 817
#> 東部 fy2018 109.3 137 40 -166.6 385
#> 中部 fy2018 301.0 111 40 75.7 526
#> 西部 fy2018 29.2 118 40 -209.7 268
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> 東部 fy1990 - 中部 fy1990 -86.4 176 40 -0.490 0.9962
#> 東部 fy1990 - 西部 fy1990 -459.3 181 40 -2.543 0.1360
#> 東部 fy1990 - 東部 fy2018 9.0 193 40 0.047 1.0000
#> 東部 fy1990 - 中部 fy2018 -182.7 176 40 -1.036 0.9027
#> 東部 fy1990 - 西部 fy2018 89.1 181 40 0.493 0.9961
#> 中部 fy1990 - 西部 fy1990 -372.8 162 40 -2.295 0.2201
#> 中部 fy1990 - 東部 fy2018 95.4 176 40 0.542 0.9940
#> 中部 fy1990 - 中部 fy2018 -96.2 158 40 -0.610 0.9897
#> 中部 fy1990 - 西部 fy2018 175.5 162 40 1.080 0.8863
#> 西部 fy1990 - 東部 fy2018 468.3 181 40 2.593 0.1226
#> 西部 fy1990 - 中部 fy2018 276.6 162 40 1.702 0.5383
#> 西部 fy1990 - 西部 fy2018 548.4 167 40 3.280 0.0245
#> 東部 fy2018 - 中部 fy2018 -191.7 176 40 -1.087 0.8835
#> 東部 fy2018 - 西部 fy2018 80.1 181 40 0.443 0.9977
#> 中部 fy2018 - 西部 fy2018 271.8 162 40 1.672 0.5573
#>
#> P value adjustment: tukey method for comparing a family of 6 estimates
emmeans(mall, specs = pairwise ~ site|year, adjust = "tukey")
#> $emmeans
#> year = fy1990:
#> site emmean SE df lower.CL upper.CL
#> 東部 118.3 137 40 -157.6 394
#> 中部 204.8 111 40 -20.5 430
#> 西部 577.6 118 40 338.7 817
#>
#> year = fy2018:
#> site emmean SE df lower.CL upper.CL
#> 東部 109.3 137 40 -166.6 385
#> 中部 301.0 111 40 75.7 526
#> 西部 29.2 118 40 -209.7 268
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> year = fy1990:
#> contrast estimate SE df t.ratio p.value
#> 東部 - 中部 -86.4 176 40 -0.490 0.8762
#> 東部 - 西部 -459.3 181 40 -2.543 0.0389
#> 中部 - 西部 -372.8 162 40 -2.295 0.0681
#>
#> year = fy2018:
#> contrast estimate SE df t.ratio p.value
#> 東部 - 中部 -191.7 176 40 -1.087 0.5273
#> 東部 - 西部 80.1 181 40 0.443 0.8976
#> 中部 - 西部 271.8 162 40 1.672 0.2282
#>
#> P value adjustment: tukey method for comparing a family of 3 estimates
emmeans(mall, specs = pairwise ~ year|site, adjust = "tukey")
#> $emmeans
#> site = 東部:
#> year emmean SE df lower.CL upper.CL
#> fy1990 118.3 137 40 -157.6 394
#> fy2018 109.3 137 40 -166.6 385
#>
#> site = 中部:
#> year emmean SE df lower.CL upper.CL
#> fy1990 204.8 111 40 -20.5 430
#> fy2018 301.0 111 40 75.7 526
#>
#> site = 西部:
#> year emmean SE df lower.CL upper.CL
#> fy1990 577.6 118 40 338.7 817
#> fy2018 29.2 118 40 -209.7 268
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> site = 東部:
#> contrast estimate SE df t.ratio p.value
#> fy1990 - fy2018 9.0 193 40 0.047 0.9631
#>
#> site = 中部:
#> contrast estimate SE df t.ratio p.value
#> fy1990 - fy2018 -96.2 158 40 -0.610 0.5451
#>
#> site = 西部:
#> contrast estimate SE df t.ratio p.value
#> fy1990 - fy2018 548.4 167 40 3.280 0.00227.9 等分散性と正規性の事後確認
plot() に渡している mall は前章に当てはめた二元配置分散分析のモデルです。
7.10 等分散性の確認に使うプロット
plot(mall, which = 1)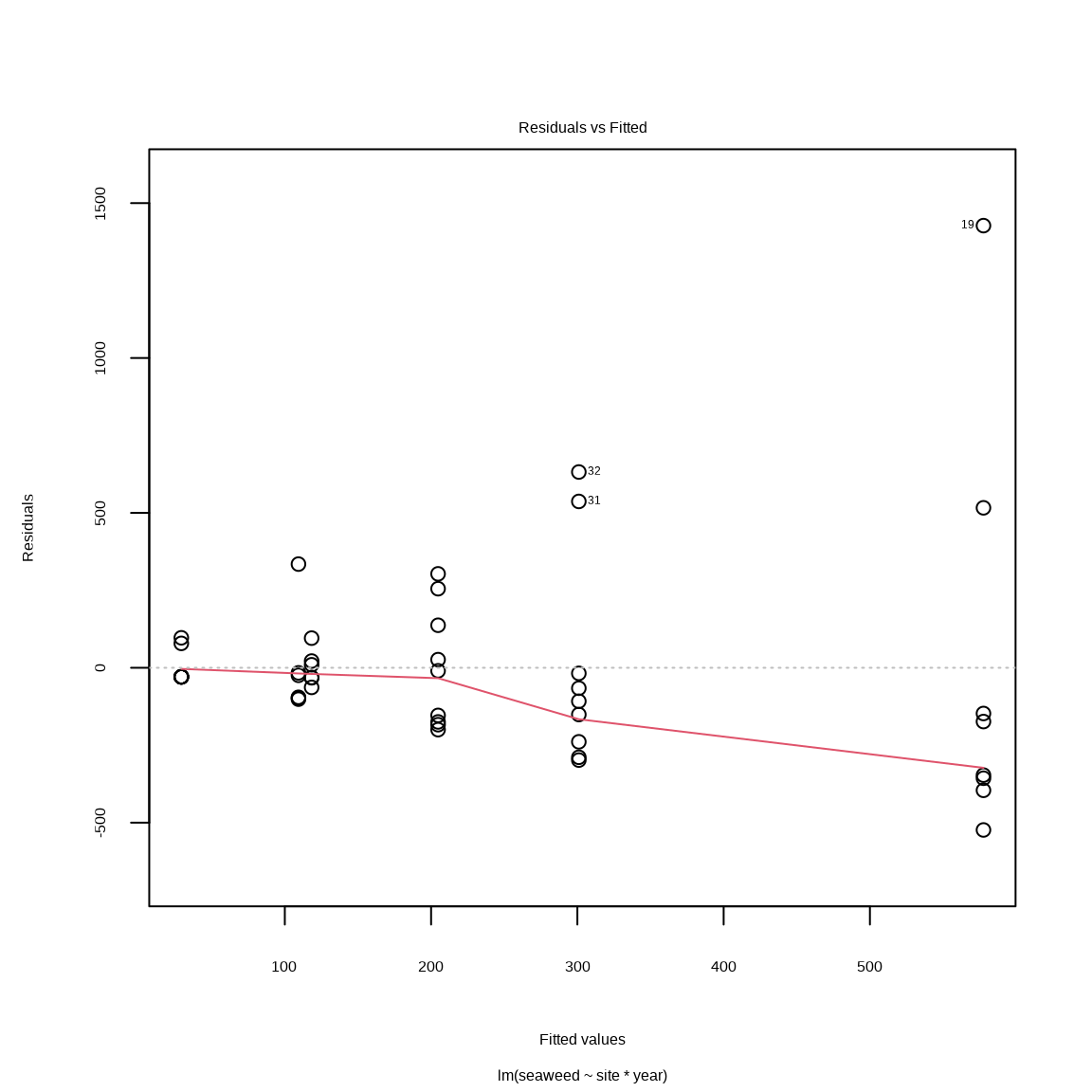
Figure 7.1: 残渣 vs. 期待値
Fig. 7.1 は残渣11 と期待値12 の関係を理解するてめに使います。 等分散性に問題がない場合、残渣は y = 0 の周りを均一に、変動なくばらつきます。 ところが Fig. 7.1 の場合、期待値が高いとき、残渣のばらつきが大きい。
plot(mall, which = 3)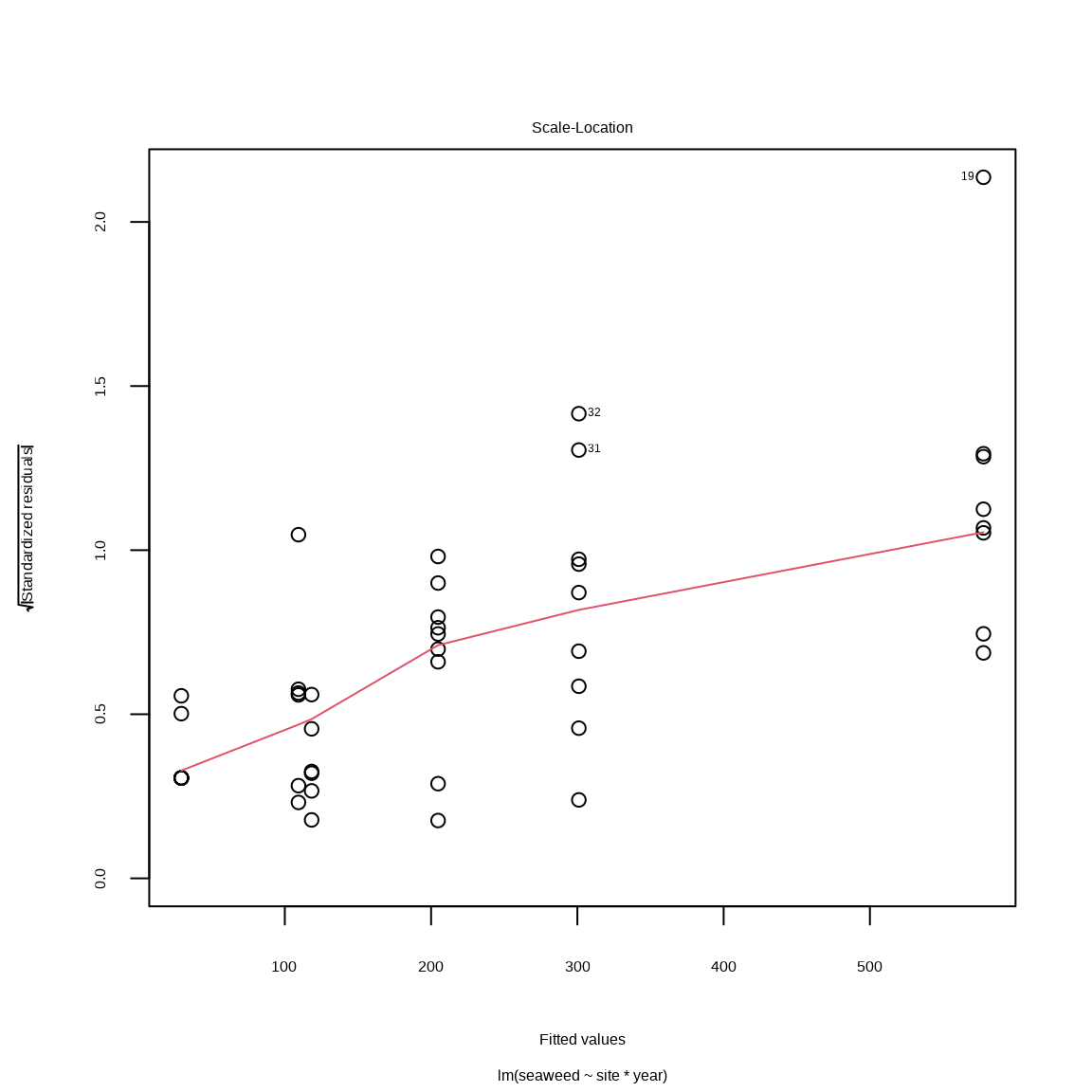
Figure 7.2: スケール・位置プロット
Fig. 7.2 はスケール・ロケーションプロットといいます。 スケール13 は確率密度分布のばらつきのパラメータです。 位置(ロケーション)14 は確率分布の中心のパラメータです。 たとえば、正規分布のスケールパラメータは分散、位置パラメータは平均値です。 Fig. 7.2 の横軸は位置、縦長はスケールパラメータで標準化した残渣の平方根です。 示されている標準化残渣のばらつきが均一で、期待値15 と無関係であれば、ばらつきは均一であると考えられます。 Fig. 7.2 の場合、標準化残渣は期待値と正の関係があるので、ばらつきは均一であると考えられません。