11 非線形モデル-I

ここで紹介する非線形モデルは、海洋生物科学実験III用に準備しました。光合成光曲線の解析を紹介します。

11.1 必要なパッケージ

library(tidyverse)
library(googlesheets4)
library(ggcorrplot)
library(patchwork)
library(minpack.lm)
library(nlstools)
library(broom)

11.2 データの読み込み

データは Google Drive に共有しています。 googlesheets4 のパッケージをつかて、データをクラウドからダウンロードできます。リンクをクリックしたら、ブラウザからもダウンロードできます。データは共有制限なしで公開したので、authentication なしでアクセスできます。このときは gs4_deauth() を実行します。

gs4_deauth()

Google Drive で共有したデータは次のURLの通りです。リンクは実験日１〜３の google sheets に飛びます。

spreadsheet1 = "https://docs.google.com/spreadsheets/d/1CsY7ILKZRFlwQEIzSgu1veMQ964IPVegIJOo04lIGVE/edit#gid=1846404397"
spreadsheet2 = "https://docs.google.com/spreadsheets/d/1yeC-rJdxdiVa_icoNHZ1xrt4HWHyGCeQMnUt1r2_hnk/edit#gid=540001236" 
spreadsheet3 = "https://docs.google.com/spreadsheets/d/1Im8Qg-ukk8uh_3z4H6IwirTc4nhxPqKrDWrjhK4gZ0o/edit#gid=2099964525"

公開した google sheets にはつぎのスプレッドシートが入っています。

光合成データ
海藻資料データ
光環境データ

データの読み込みは read_sheet() で行います。各シートの構造は同じにしたので、map() をつかって一度にデータを読み込みます。 fnames 変数は解析に使わないので、select(-fnames) で外します。

mgldata = tibble(fnames = c(spreadsheet1, spreadsheet2, spreadsheet3), day = 1:3) |> 
  mutate(data = map(fnames, read_sheet, sheet = "光合成データ")) |> 
  select(-fnames)
seaweed = tibble(fnames = c(spreadsheet1, spreadsheet2, spreadsheet3), day = 1:3) |> 
  mutate(data = map(fnames, read_sheet, sheet = "海藻資料データ"))|> 
  select(-fnames)
lightdata = tibble(fnames = c(spreadsheet1, spreadsheet2, spreadsheet3), day = 1:3) |> 
  mutate(data = map(fnames, read_sheet, sheet = "光環境データ"))|> 
  select(-fnames)

11.2.1 光環境データの処理

光条件毎の (light) 光量子量 (ppfd) の平均値を求めます。 アルミホイル の光条件のときの光量子量は測っていないが、ppfd は 0 とします。 アルミホイル のときのデータはコードとして定義して、追加します。

lightdata = lightdata |> 
  unnest(data) |> 
  select(day,
         han = "班",
         light = "光環境",
         sample = matches("サンプル"),
         ppfd = matches("光量子")) |> 
  group_by(day, light) |> 
  summarise(ppfd = mean(ppfd))

アルミホイルのデータを定義し、tmp に入れます。

tmp = tibble(light = rep("アルミホイル",3), 
             ppfd =  rep(0, 3),
             day = 1:3)

観測したデータと tmp を縦に結合します。

lightdata = bind_rows(lightdata, tmp) |> 
  mutate(light = factor(light), day = factor(day))

11.2.2 全データを結合

光合成データ mgldata と海藻資料データ seaweed を結合します。 matches() は select() の selection helper function です。 matches() にわたした正規表現 (regular expression) とマッチ (match) した変数（列名）が返ってきます。

mgldata = mgldata |> unnest(data) |> 
  select(day,
         han = "班",
         sample = matches("サンプル"),
         min = matches("時間"),
         mgl = matches("酸素"),
         temperature = matches("水温"),
         light = matches("光環境"),
         seaweed = matches("海藻"))

seaweed = seaweed |> unnest(data) |> 
  select(day,
         seaweed = matches("海藻"),
         han = "班",
         sample = matches("サンプル"),
         vol = matches("容量"),
         gww = matches("湿重量"))

mgldata = full_join(mgldata, seaweed, by = c("han", "sample", "day"))

han, sample, day は as.factor() を通して因子に変換します。 across() は複数変数に同じ関数を適応したいときにつかいます。

mgldata = mgldata |> mutate(across(c(han, sample, day), as.factor))

across() を使わずに変換するなら、次通りです。

mgldata = mgldata |>
  mutate(han = as.factor(han), sample = as.factor(sample), day = as.factor(day))

結合したら，溶存酸素濃度の時間変動を可視化します。

ggplot(mgldata) +
  geom_point(aes(x = min, y = mgl, color = han)) +
  facet_grid(rows = vars(light),
             cols = vars(seaweed))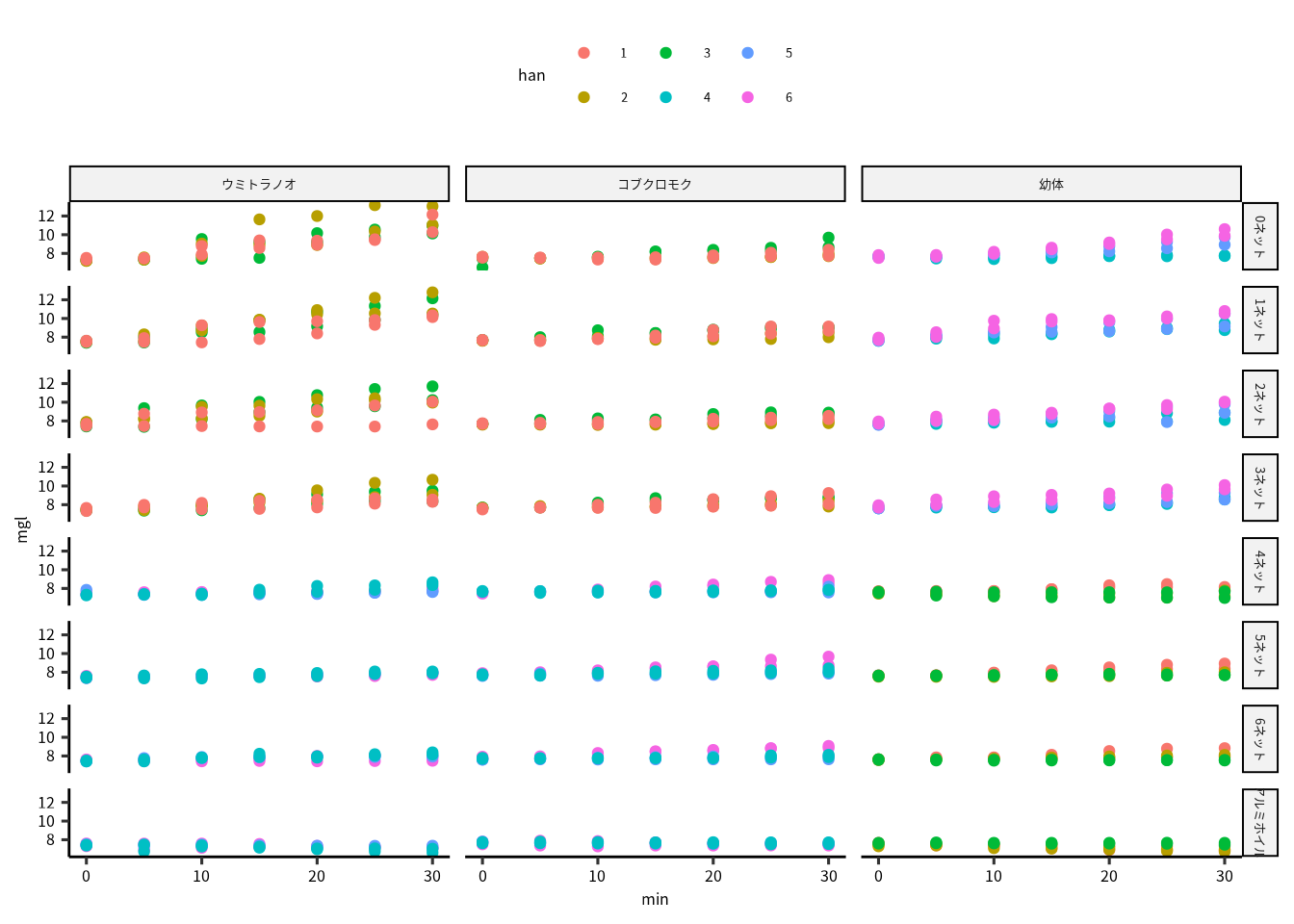

光の調整は編み袋 (ネット) でやっています。ネットの枚数が増えると光量子量が下がります。アルミホイルで光量子量が 0 の条件を作っています。ネットがないとき (最も明るいとき) 溶存酸素濃度が顕著に増加しましたが、アルミホイルのときは緩やかに減少しました。

11.2.3 光合成速度を求める

複数データ群から光合成速度を計算したいので、map() 関数を通して行います。 map() に渡す光合成速度用関数を定義します。 fit_model() は線形モデルを溶存酸素濃度時系列データに当てはめ用です。 get_rate() は 2 つのモデル係数 \((y = b_0+ b_1 x)\) から傾き \((b_1)\) を抽出します。

fit_model = function(df) {
  lm(mgl ~ min, data = df)
}
get_rate = function(m) {
  coefficients(m)[2] 
}

ここでデータをグループ化して、グループ毎の傾きを求めます。

mgldata = 
  mgldata |> 
  group_nest(day, han, sample, light, gww, vol, seaweed) |> 
  mutate(model = map(data, fit_model)) |> 
  mutate(rate = map_dbl(model, get_rate)) |> 
  mutate(stats = map(model, glance)) |> 
  unnest(stats)

求めた係数と環境データを結合します。

alldata = full_join(mgldata, lightdata, by = c("day", "light"))

係数は湿重量を実験容器の容積で割って、湿重量あたりの純光合成速度を求めます。ここで、係数の単位は mg O₂ l^-1 min^-1 から mg O₂ g_ww^{-1}min-1^ に変わります。

単位の求め方：

\[ \overbrace{\frac{mg\;\text{O}_2}{l}}^{\text{酸素濃度}} \times \underbrace{\frac{1}{g_{ww}}}_{\text{湿重量}} \times \overbrace{ml}^{\text{容積}} \times \frac{1 \;l}{1000\; ml} \times \frac{1000\;\mu g\;\text{O}_2}{1\;mg\;\text{O}_2} \] R コード：

alldata = 
  alldata %>% 
  mutate(normalized_rate = rate / gww * vol)

解析をする前に、光量子量、種、班ごとの平均値を求めます。

dataset = 
  alldata |> 
  group_by(ppfd, seaweed, han) |> 
  summarise(np = mean(normalized_rate))

標準化した光合成速度は次の通りです。

xlabel = expression(paste("PPFD"~(mu*mol~m^{-2}~s^{-1})))
ylabel = '"Net photosynthesis rate"~(mu*g~O[2]~g[ww]^{-1}~min^{-1})'
ylabel = as.expression(parse(text = ylabel))
dataset |> 
  ggplot() + 
  geom_point(aes(x = ppfd, y = np, color = han)) +
  scale_color_viridis_d("", end = 0.8) +
  scale_x_continuous(xlabel) +
  scale_y_continuous(ylabel) +
  facet_grid(col = vars(seaweed))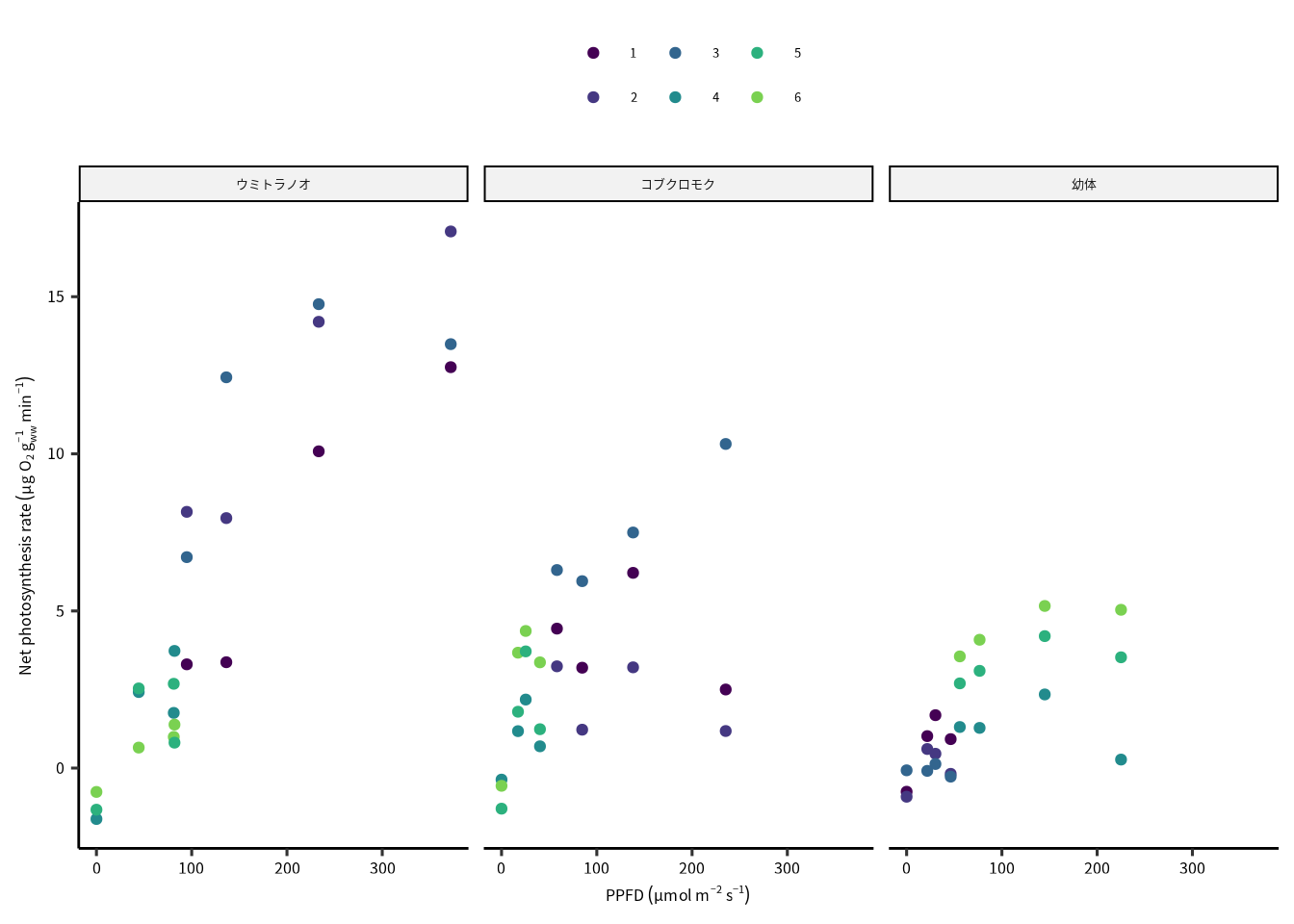

Figure 11.1: ウミトラノオ、コブクロモク、ホンダワラ属海藻の幼体の光合成速度。記号の色はそれぞれの班を示しています。光合成速度のばらつきは光量子量があると大きくなるのが明らかです。

11.3 モデルの当てはめ

非線形モデルの当てはめに便利な nlstools パッケージを使います。

library(nlstools)

当てはめたいモデルは次のとおりです。

\[ \overbrace{P_{net}}^{\text{純光合成速度}} = \underbrace{P_{max}\left(1 - \exp\left(-\frac{\alpha}{P_{max}}I\right)\right)}_{\text{総光合成速度}} - \overbrace{R_d}^{\text{暗呼吸速度}} \]

\(P_{net}\) は純光合成速度 (normalized_rate)
\(I\) は光量子量 (ppfd)
\(P_{max}\) は光合成飽和速度 (pmax)
\(\alpha\) は初期勾配 (alpha)
\(R_d\) は暗呼吸速度 (rd)

このモデルをR関数に書き換えると次のようになります。

pecurve = function(ppfd, pmax, rd, alpha) {
  pmax * (1-exp(-alpha / pmax * ppfd)) - rd
}

nlstools の preview() 関数をつかって，モデル当てはめ用の関数 (nls()) に必要なの初期値を探します。 variable 引数に ppfd 変数の位置情報を渡してください。この位置情報は tibble 変数（列）の順位です。このデータの場合、ppfd は 1 列目なので、variable = 1 を preview() に渡しています。 str_detect() も matches() と同じように正規表現をつかって、 seaweed 変数からマッチしたものを返します。

START = list(pmax = 10, rd = 3, alpha = 0.3)

crispifolium = dataset |> filter(str_detect(seaweed, "コブクロ"))
thunbergii   = dataset |> filter(str_detect(seaweed, "ウミトラノオ"))
juvenile     = dataset |> filter(str_detect(seaweed, "幼体"))

preview(np ~ pecurve(ppfd, pmax, rd, alpha), 
        data = crispifolium, 
        variable = 1,
        start = START)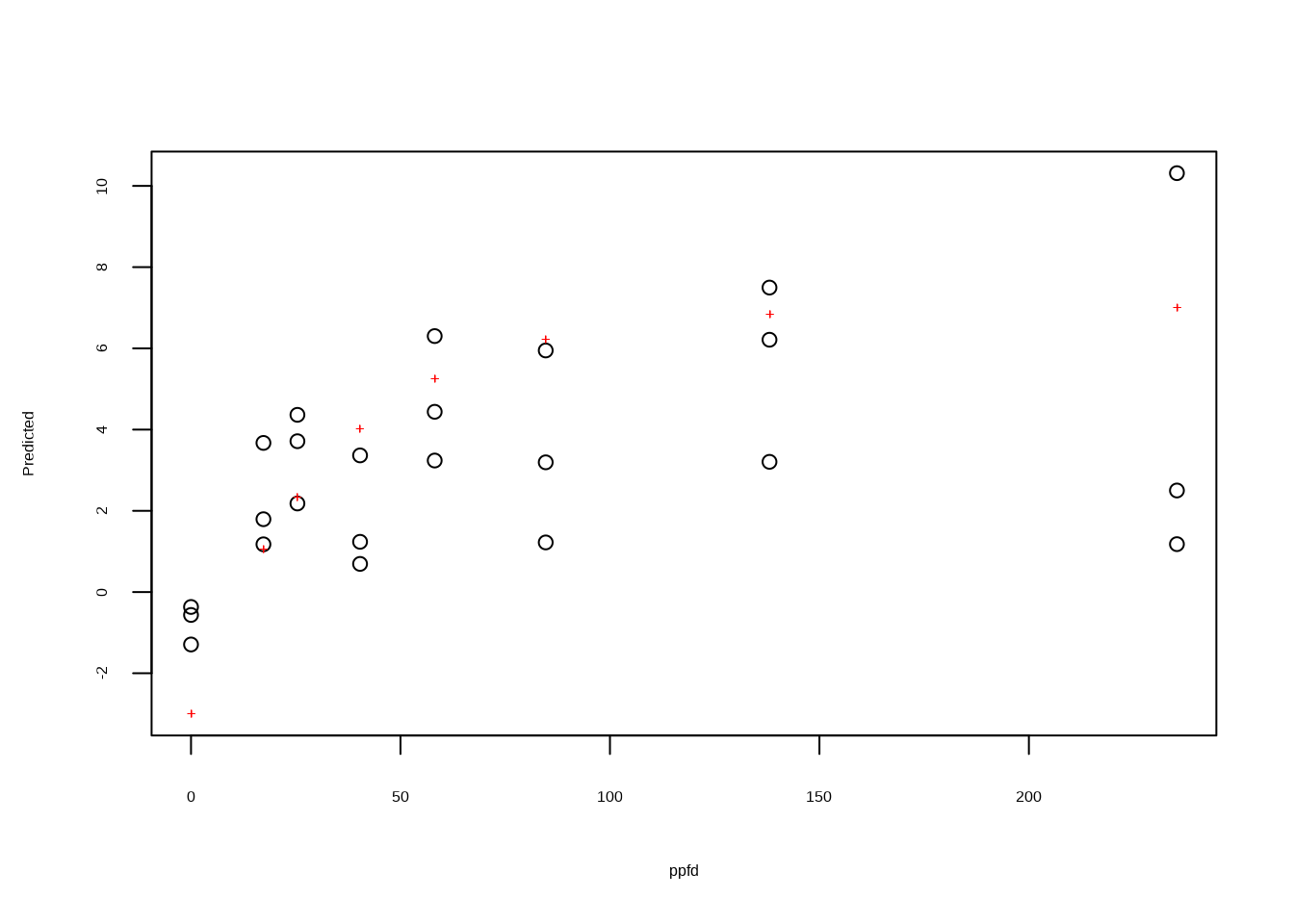

#> 
#> RSS:  167

preview(np ~ pecurve(ppfd, pmax, rd, alpha), 
        data = thunbergii, 
        variable = 1,
        start = START)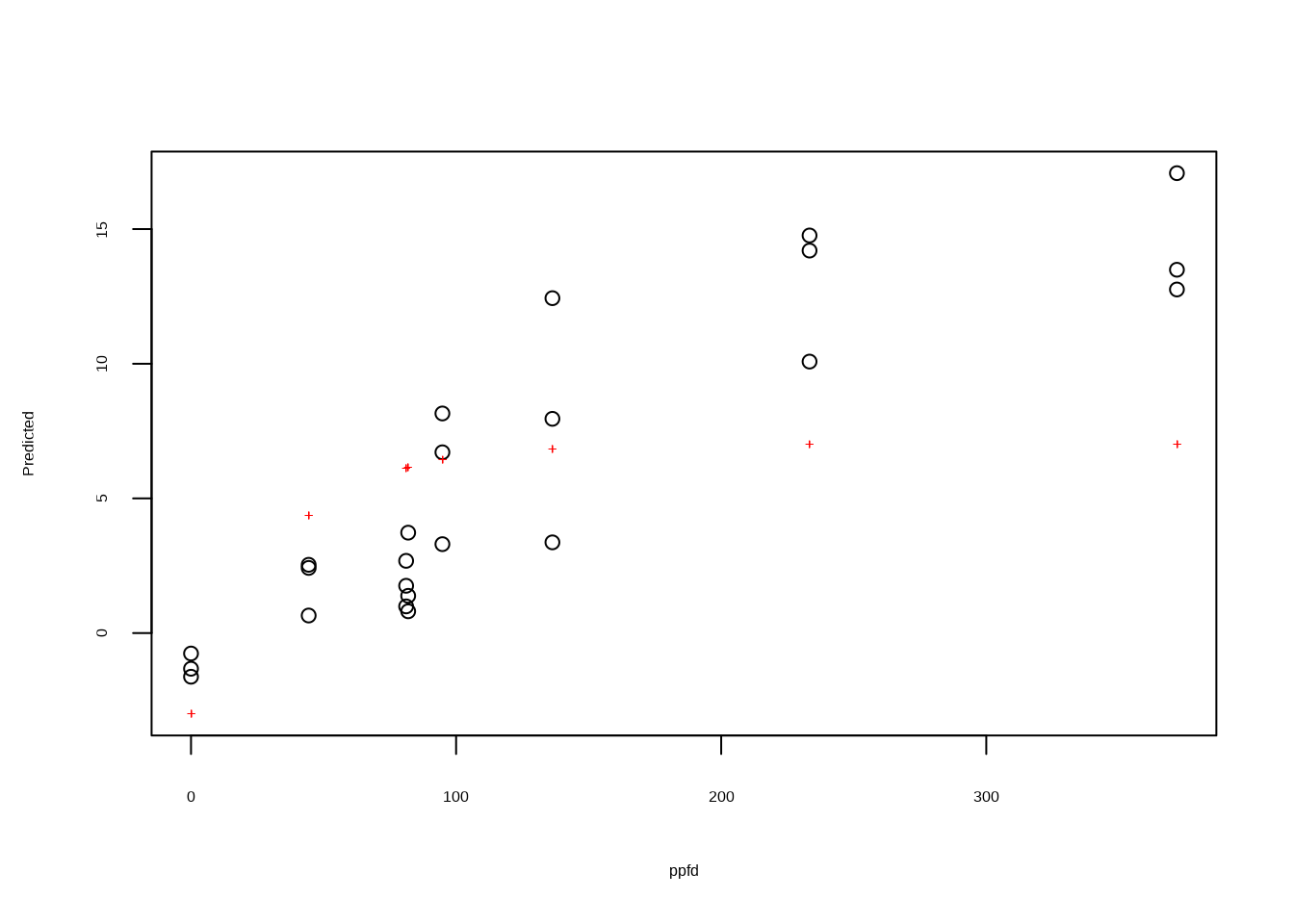

#> 
#> RSS:  501

preview(np ~ pecurve(ppfd, pmax, rd, alpha), 
        data = juvenile, 
        variable = 1,
        start = START)

#> 
#> RSS:  246

+ 記号がデータの中心に通る用になったら，そのときの初期値を nls() または、minpack.lm パッケージの nlsLM() 関数に渡してモデルの当てはめをします。 nls() 関数は Gauss-Newton アルゴリズムによってパラメータ推定をしますが、nlsLM() は Levenberg-Marquardt アルゴリズムを用います。 Levenberg-Marquardt法のほうが優秀ですが、モデルの組み方によって使えないときがあります。

ここではデータを海藻毎に当てはめるので、解析関数をつくります。

fit_nls = function(df) {
  START = list(pmax = 14, rd = 3, alpha = 0.3)
  # nls(np ~ pecurve(ppfd, pmax, rd, alpha),  data = df, start = START)
  nlsLM(np ~ pecurve(ppfd, pmax, rd, alpha),  data = df, start = START)
}

dataset = dataset |> ungroup() |> 
  group_nest(seaweed) |>
  mutate(model = map(data, fit_nls))
dataset
#> # A tibble: 3 × 3
#>   seaweed                    data model 
#>   <chr>        <list<tibble[,3]>> <list>
#> 1 ウミトラノオ           [24 × 3] <nls> 
#> 2 コブクロモク           [24 × 3] <nls> 
#> 3 幼体                   [24 × 3] <nls>

当てはめたモデルの結果は次の通りです。

dataset = dataset |> 
  mutate(summary =map(model, glance)) |> 
  unnest(summary)
dataset
#> # A tibble: 3 × 12
#>   seaweed       data model sigma isConv  finTol logLik   AIC
#>   <chr>     <list<t> <lis> <dbl> <lgl>    <dbl>  <dbl> <dbl>
#> 1 ウミトラ… [24 × 3] <nls>  2.51 TRUE   1.49e-8  -54.5 117. 
#> 2 コブクロ… [24 × 3] <nls>  2.21 TRUE   1.49e-8  -51.5 111. 
#> 3 幼体      [24 × 3] <nls>  1.31 TRUE   1.49e-8  -39.0  86.0
#> # … with 4 more variables: BIC <dbl>, deviance <dbl>,
#> #   df.residual <int>, nobs <int>

次はモデルの期待値を求めます。この関数は期待値を擬似データから計算します。擬似データは tibble() で作っています。

calc_fitted = function(data, model) {
  N = 21 # 擬似データの長さ
  ndata = tibble(ppfd = seq(min(data$ppfd), max(data$ppfd),length = N))
  tmp = predict(model, newdata = ndata) |> as_tibble()
  bind_cols(ndata,tmp)
}

dataset = dataset |> mutate(fitted = map2(data, model, calc_fitted))

ggplot() +
  geom_point(aes(x = ppfd, y = np), data = unnest(dataset, data))+
  geom_line(aes(x = ppfd, y = value), data = unnest(dataset, fitted)) +
  facet_grid(rows = vars(seaweed))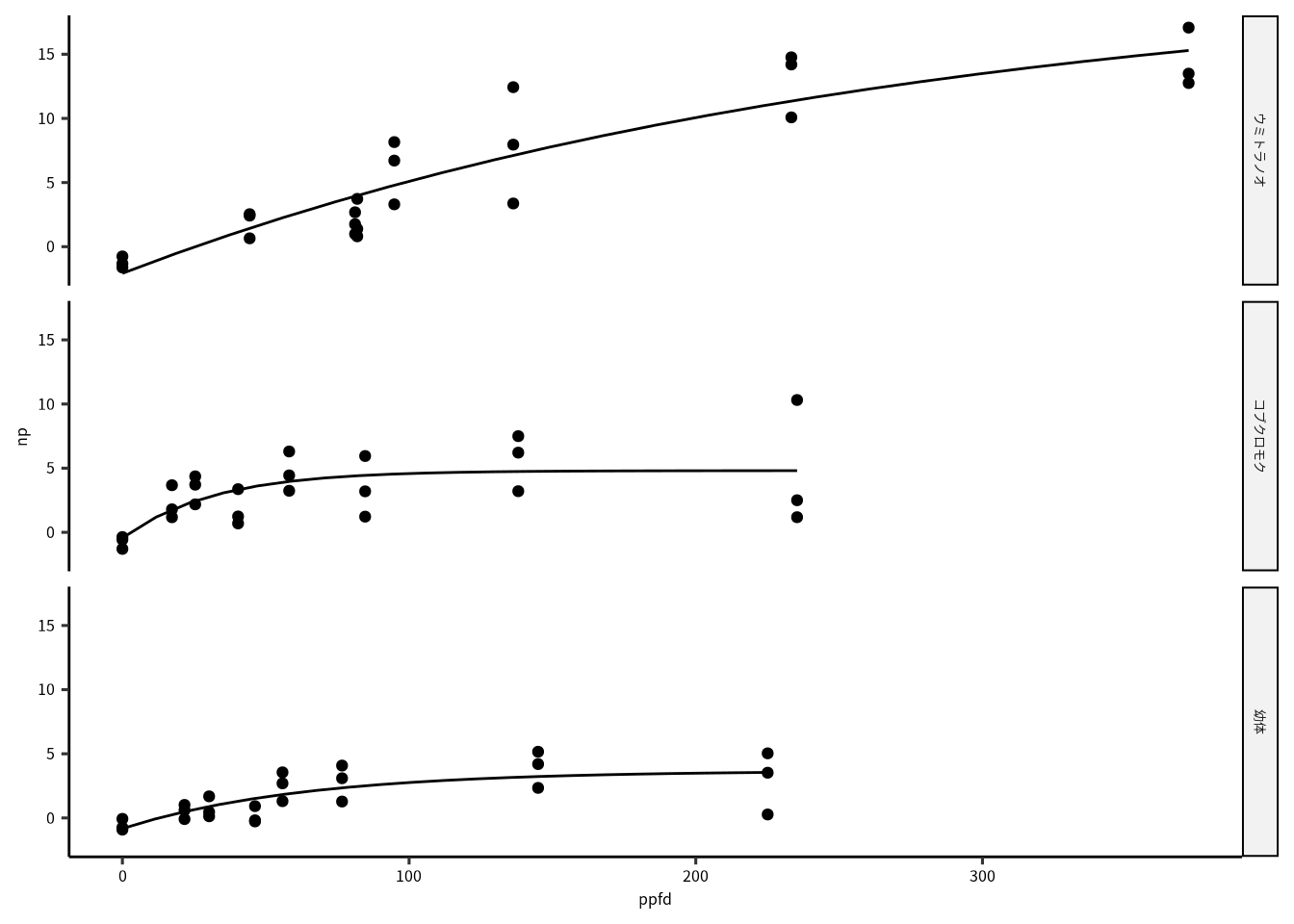

Figure 11.2: 観測とモデル期待値。

11.4 診断図

線形モデルと同様に、モデルを当てはめたら、残渣の診断図も確認します。ここでは残渣 (residuals) とモデル期待値 (fitted) を求めます。

shindan = dataset |> 
  select(seaweed, data, model) |> 
  mutate(residuals = map(model, residuals)) |> 
  mutate(fitted = map(model, fitted)) |> 
  select(seaweed, data, residuals, fitted) |> 
  unnest(everything())

p1 = ggplot(shindan) +
  geom_point(aes(x = fitted, y = residuals,
                 color = seaweed),
             size = 3) +
  geom_hline(yintercept = 0, linetype = "dashed") +
  scale_color_viridis_d(end = 0.8)

p2 = ggplot(shindan) +
  geom_point(aes(x = fitted, y = sqrt(abs(residuals)),
                 color = seaweed),
             size = 3) +
  scale_color_viridis_d(end = 0.8)
p1+p2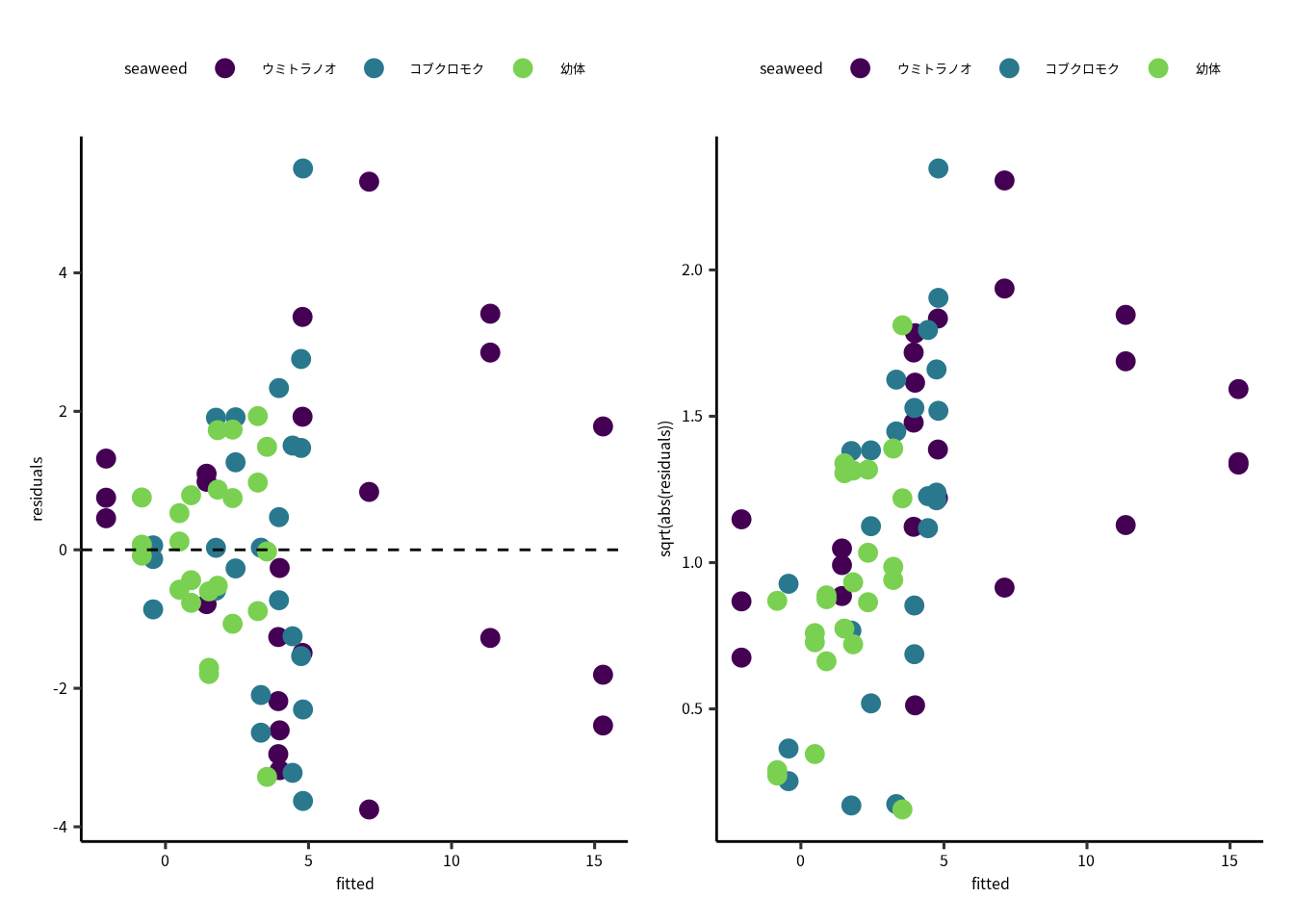

モデル残渣と残渣の絶対値の平方根の図で、モデルの当てはめの良さが分かります。
（左）はモデル残渣対期待値です。期待値が増加するとモデル残渣の散らばりが大きくなるのがはっきりしています。
点線 (0) の周りを均一にばらつくのが理想です。
（右）は残渣の絶対値の平方根です。期待値が上がると残渣が増加しています。
これらの図を確認すると、残渣のばらつきの均一性に問題があります。

Figure 11.3: モデル残渣と残渣の絶対値の平方根の図で、モデルの当てはめの良さが分かります。（左）はモデル残渣対期待値です。期待値が増加するとモデル残渣の散らばりが大きくなるのがはっきりしています。点線 (0) の周りを均一にばらつくのが理想です。（右）は残渣の絶対値の平方根です。期待値が上がると残渣が増加しています。これらの図を確認すると、残渣のばらつきの均一性に問題があります。

11.5 パラメータの集計

残渣プロットの結果はひどかったが、とりあえず、光飽和点 \((I_k)\) と光補償点 \((I_c)\) を求めましょう。

光飽和点：\(I_k = P_{max} / \alpha\)
光補償点：\(I_c = \frac{P_{max}}{\alpha} \ln\left(\frac{P_{max}}{P_{max} - R_d}\right)\)

まずは係数を抽出するための関数を定義します。モデルの定義によって、cfs からパラメータを抽出すろときのコードが変わります。 pecurve() を定義したときに、pmax, alpha, rd がパラメータ名だったので、抽出には "pmax", "alpha", "rd" の文字列を使いました。文字列はパラメータ名と一致するようにしましょう。

get_cfs = function(m) {
  cfs = coef(m)
  tibble(pmax = cfs["pmax"],
         alpha = cfs["alpha"],
         rd = cfs["rd"])
}

ここで光飽和点と光補償点を求めるための関数を定義します。

calc_ik = function(m) {
  # 光飽和点
  cfs = coef(m)
  cfs["pmax"] / cfs["alpha"]*log(cfs["pmax"]/(cfs["pmax"] - cfs["rd"]))
}
calc_ic = function(m) {
  # 光補償点
  cfs = coef(m)
  cfs["pmax"] / cfs["alpha"]
}

map() を使って係数を求めます。

modelcfs = dataset %>% 
  select(seaweed, model) |> 
  mutate(cfs = map(model, get_cfs)) |> 
  mutate(ik = map(model, calc_ik)) |> 
  mutate(ic = map(model, calc_ic)) |> 
  unnest(c(ik, ic, cfs))
modelcfs
#> # A tibble: 3 × 7
#>   seaweed      model   pmax  alpha    rd    ik    ic
#>   <chr>        <list> <dbl>  <dbl> <dbl> <dbl> <dbl>
#> 1 ウミトラノオ <nls>  23.3  0.0858 2.08  25.4  271. 
#> 2 コブクロモク <nls>   5.24 0.165  0.431  2.74  31.8
#> 3 幼体         <nls>   4.50 0.0718 0.827 12.7   62.7

海藻類	P_max	α	R_d	I_k	I_c
ウミトラノオ	23.3	0.086	2.1	25.4	271.4
コブクロモク	5.2	0.165	0.4	2.7	31.8
幼体	4.5	0.072	0.8	12.7	62.7

11.5.1 モデル係数表について

モデル係数の統計量は summary() または nlstools の overview() で見れます。 Estimate はモデル係数の期待値です。 Std. Error は係数の標準誤差です。 t value と Pr(>|t|) は 0 に対して、モデル係数の t 値と t 値の P 値です。この係数結果に出力されたものが Wald’s test の結果です。すべての海藻類に対して、\(P_{max} = 0\) の帰無仮説を棄却できますが、 \(R_d = 0\) の帰無仮説は棄却できません。コブクロモクと幼体の \(\alpha = 0\) の帰無仮説は棄却できないが、ウミトラノオの場合は棄却できました。

dataset |> 
  mutate(summary = map(model, summary)) |> 
  pull(summary, name = seaweed)
#> $ウミトラノオ
#> 
#> Formula: np ~ pecurve(ppfd, pmax, rd, alpha)
#> 
#> Parameters:
#>       Estimate Std. Error t value Pr(>|t|)    
#> pmax  23.28655    5.72475   4.068 0.000553 ***
#> rd     2.07666    1.27193   1.633 0.117440    
#> alpha  0.08580    0.02415   3.553 0.001883 ** 
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.506 on 21 degrees of freedom
#> 
#> Number of iterations to convergence: 9 
#> Achieved convergence tolerance: 1.49e-08
#> 
#> 
#> $コブクロモク
#> 
#> Formula: np ~ pecurve(ppfd, pmax, rd, alpha)
#> 
#> Parameters:
#>       Estimate Std. Error t value Pr(>|t|)   
#> pmax    5.2410     1.3996   3.745  0.00119 **
#> rd      0.4315     1.2211   0.353  0.72736   
#> alpha   0.1646     0.1069   1.539  0.13862   
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.212 on 21 degrees of freedom
#> 
#> Number of iterations to convergence: 7 
#> Achieved convergence tolerance: 1.49e-08
#> 
#> 
#> $幼体
#> 
#> Formula: np ~ pecurve(ppfd, pmax, rd, alpha)
#> 
#> Parameters:
#>       Estimate Std. Error t value Pr(>|t|)    
#> pmax   4.50104    0.92297   4.877 8.02e-05 ***
#> rd     0.82731    0.69152   1.196   0.2449    
#> alpha  0.07176    0.03480   2.062   0.0518 .  
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.314 on 21 degrees of freedom
#> 
#> Number of iterations to convergence: 10 
#> Achieved convergence tolerance: 1.49e-08

11.6 多重比較

数種類のデータ群に、一つのモデルを当てはめたら、群毎に推定したパラメータの違いが気になります。複数群をお互いに比較することは多重比較といいます。一般的には、群毎にパラメータを推定する full model から群毎のデータをまとめて、一つのパラメータを推定する pooled model まで考えられます。このとき、nlsLM() は使用できないので、nls() 関数を使います。 nls() の収束を助けるために、まずは pooled model の nlsLM() の結果を full model のパラメータ初期値にします。

では、データをすこし整理します。

dataset = dataset |> select(seaweed, data) |> unnest(data)
dataset = dataset |> mutate(seaweed = factor(seaweed))

フルモデル (full model) の場合は群毎に、\(P_{max}\)、\(\alpha\)、\(R_d\) を推定します。プールモデル (pooled model) の場合は、群の区別をせず、1 セットのパラメータを推定します。

# フルモデルの初期値を求める
poolmodel = nlsLM(np ~ pecurve(ppfd, pmax, rd, alpha), 
                  start = list(pmax = 10, rd = 3, alpha = 0.3),
                  data = dataset, 
                  lower = c(pmax = 0, rd = 0, alpha = 0))

nlsLM() は次のようにインデックスされた係数のモデルに対応していないので、nls() を使います。

START = lapply(coef(poolmodel), rep, 3)
fullmodel = nls(np ~ pecurve(ppfd, pmax[seaweed], rd[seaweed], alpha[seaweed]), 
                start = START, 
                data = dataset)

AIC を確認すると、フルモデルの AIC が最も低いです。

AIC(poolmodel, fullmodel) |> as_tibble(rownames = "model") |> arrange(AIC)
#> # A tibble: 2 × 3
#>   model        df   AIC
#>   <chr>     <dbl> <dbl>
#> 1 fullmodel    10  320.
#> 2 poolmodel     4  353.

すべてのモデルを当てはめて、AIC で比較することはできます。 3 変数・3 群のモデルの組み方は \((3(3-1)/2)^3=125\) とおりも考えられます。 125とおりのモデルを調べたくないので、Wald’s 検定でパラメータ比較をします。

【重要】：ここで評価したフルモデルと海藻毎に当てはめたモデルのモデル係数に期待値は同じじゃない！

summary(fullmodel)
#> 
#> Formula: np ~ pecurve(ppfd, pmax[seaweed], rd[seaweed], alpha[seaweed])
#> 
#> Parameters:
#>        Estimate Std. Error t value Pr(>|t|)    
#> pmax1  23.28613    4.73717   4.916 6.64e-06 ***
#> pmax2   5.24099    1.31169   3.996 0.000172 ***
#> pmax3   4.50104    1.45692   3.089 0.002983 ** 
#> rd1     2.07673    1.05259   1.973 0.052890 .  
#> rd2     0.43151    1.14443   0.377 0.707404    
#> rd3     0.82730    1.09158   0.758 0.451339    
#> alpha1  0.08580    0.01999   4.293 6.20e-05 ***
#> alpha2  0.16462    0.10022   1.643 0.105444    
#> alpha3  0.07176    0.05493   1.306 0.196200    
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 2.073 on 63 degrees of freedom
#> 
#> Number of iterations to convergence: 14 
#> Achieved convergence tolerance: 5.833e-06

推定した係数の違いはモデルの構造と関係しています。それぞれの海藻に当てはめたとき、それぞれの海藻のモデルごとに独立した誤差項が存在するが、上のフルモデルの場合 1 つの誤差項しかないです。

つまり、それぞれの海藻にはつぎのモデルを当てはめたので、\(\sigma\) 3 つ存在します。これで、係数の期待値と標準誤差がきまります。

\[ \begin{aligned} \mu &= P_{max} \left(1 - \exp\left(-\frac{\alpha}{P_{max}}I\right)\right)-R_d \\ P_{net} & \sim N(\mu, \sigma) \end{aligned} \] フルモデルは次のようになります。

\[ \begin{aligned} \mu_i &= P_{max,i} \left(1 - \exp\left(-\frac{\alpha_{i}}{P_{max,i}}I\right)\right)-R_{d,i} \\ P_{net,i} & \sim N(\mu_i, \sigma) \end{aligned} \] \(i\) は海藻を区別するためのインデックス。このモデルには 1 つの \(\sigma\) しかないです。

この微妙な違いで、係数の期待値と標準誤差が変わります。

パラメータの多重比較は aomisc のパッケージが有ると楽です。インストール方法は remotes パッケージをつかって、github からインストールします。

remotes::install_github("onofriAndreaPG/aomisc")

aomisc パッケージの多重比較は Holm法を使います。

Holm 法は p 値を小さい順になれべてから実施します。最も小さい P 値の有意水準は \(\alpha / N\) です。 \(N\) は比較する回数です。ここで \(P \leq \alpha / N\) なら、次の P 値を \(\alpha / (N-1)\) で評価します。 \(P > \alpha / (N-1)\) なら、ここで検定が終わります。帰無仮説を棄却できないまで、\(N-k\) の補正で P 値を評価続けます。

library(aomisc)
cfs = summary(fullmodel)$coef
df = summary(fullmodel)$df

pmax の多重比較は次のとおりです。 3つ目の比較まで評価しました

rows = 1:3
pairComp(cfs[rows,1], cfs[rows,2],dfr = df[2], adjust = "holm")
#> $pairs
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Linear Hypotheses:
#>                  Estimate Std. Error t value Pr(>|t|)   
#> pmax1-pmax2 == 0   18.045      4.915   3.671  0.00102 **
#> pmax1-pmax3 == 0   18.785      4.956   3.790  0.00102 **
#> pmax2-pmax3 == 0    0.740      1.960   0.377  0.70711   
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> (Adjusted p values reported -- holm method)
#> 
#> 
#> $Letters
#>            Mean       SE CLD
#> pmax1 23.286128 4.737174   a
#> pmax2  5.240990 1.311692   b
#> pmax3  4.501039 1.456917   b

alphaとrdの場合、\(P > \alpha/N\) ので、3つ目比較までしません。

rows = 4:6
pairComp(cfs[rows,1], cfs[rows,2],dfr = df[2], adjust = "holm")
#> $pairs
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Linear Hypotheses:
#>              Estimate Std. Error t value Pr(>|t|)
#> rd1-rd2 == 0   1.6452     1.5549   1.058    0.882
#> rd1-rd3 == 0   1.2494     1.5164   0.824    0.882
#> rd2-rd3 == 0  -0.3958     1.5815  -0.250    0.882
#> (Adjusted p values reported -- holm method)
#> 
#> 
#> $Letters
#>          Mean       SE CLD
#> rd1 2.0767329 1.052591   a
#> rd2 0.4315057 1.144426   a
#> rd3 0.8273007 1.091576   a

rows = 7:9
pairComp(cfs[rows,1], cfs[rows,2],dfr = df[2], adjust = "holm")
#> $pairs
#> 
#>   Simultaneous Tests for General Linear Hypotheses
#> 
#> Linear Hypotheses:
#>                    Estimate Std. Error t value Pr(>|t|)
#> alpha1-alpha2 == 0 -0.07882    0.10219  -0.771        1
#> alpha1-alpha3 == 0  0.01404    0.05846   0.240        1
#> alpha2-alpha3 == 0  0.09286    0.11428   0.813        1
#> (Adjusted p values reported -- holm method)
#> 
#> 
#> $Letters
#>              Mean         SE CLD
#> alpha1 0.08579966 0.01998607   a
#> alpha2 0.16461744 0.10021636   a
#> alpha3 0.07175792 0.05493227   a

aomisc パッケージを読み込むと、drc と MASS パッケージも同時に読み込まれます。 tidyverse を読み込んだあとに、MASS パッケージを読み込むと MASS の select() 関数が定義され、 tidyverse の select() が使えなくなります。 aomisc は不要になったので、次の 3 つのパッケージをディタッチ (detach, unload) します。

detach(package:aomisc)
detach(package:drc)
detach(package:MASS)

11.7 モデル係数の相関関係

上で多重比較をしましたが、非線形モデルのパラメータはお互いとの相関関係が強いことが多いです。このとき、多重比較にバイアス (bias) が入り、フェアな比較はできません。光合成光曲線の解析から推定したパラメータの相関関係は次の図の通りです。

fm_cov  = vcov(fullmodel) # モデルパラメータの分散共分散行列
fm_corr = cov2cor(fm_cov) # モデルパラメータの相関行列

vname1 = str_c(c("pmax", "alpha", "rd"), "1")
vname2 = str_c(c("pmax", "alpha", "rd"), "2")
vname3 = str_c(c("pmax", "alpha", "rd"), "3")
p1 = ggcorrplot(fm_corr[vname1, vname1],     type = "upper", show.diag = T, lab =T)
p2 = ggcorrplot(fm_corr[vname2, vname2], type = "upper", show.diag = T, lab = T)
p3 = ggcorrplot(fm_corr[vname3, vname3], type = "upper", show.diag = T, lab = T)
p1 + p2 + p3 + plot_layout(ncol = 1)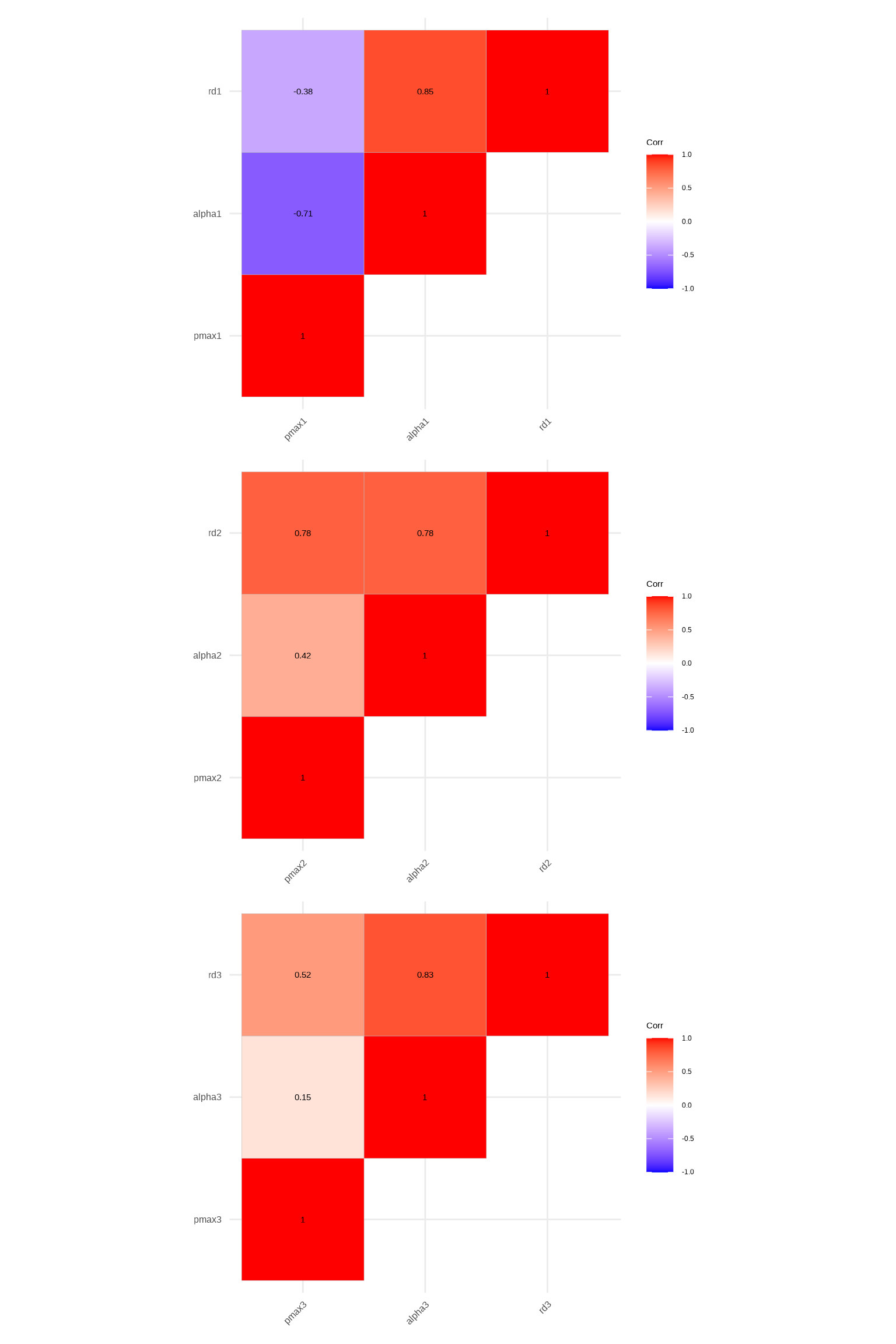

光合成光曲線の解析からもとめたパラメータの相関関係を示しています。
種ごとにまとめて、3つの相関プロットに示した。
（右）ウミトラノオ、（中）コブクロモク、（左）幼体。
相関係数は -1 から　1 をとります。
ウミトラノオ以外の場合では、パラメータごとの関係に正の相関があります。

Figure 11.4: 光合成光曲線の解析からもとめたパラメータの相関関係を示しています。種ごとにまとめて、3つの相関プロットに示した。（右）ウミトラノオ、（中）コブクロモク、（左）幼体。相関係数は -1 から　1 をとります。ウミトラノオ以外の場合では、パラメータごとの関係に正の相関があります。

vname1 = str_c(c("pmax", "alpha", "rd"), "1")
vname2 = str_c(c("pmax", "alpha", "rd"), "2")
vname3 = str_c(c("pmax", "alpha", "rd"), "3")
p1 = ggcorrplot(fm_cov[vname1, vname1],     type = "upper", show.diag = T, lab =T, legend.title = "Cov")
p2 = ggcorrplot(fm_cov[vname2, vname2], type = "upper", show.diag = T, lab = T, legend.title = "Cov")
p3 = ggcorrplot(fm_cov[vname3, vname3], type = "upper", show.diag = T, lab = T, legend.title = "Cov")
p1 + p2 + p3 + plot_layout(ncol = 1)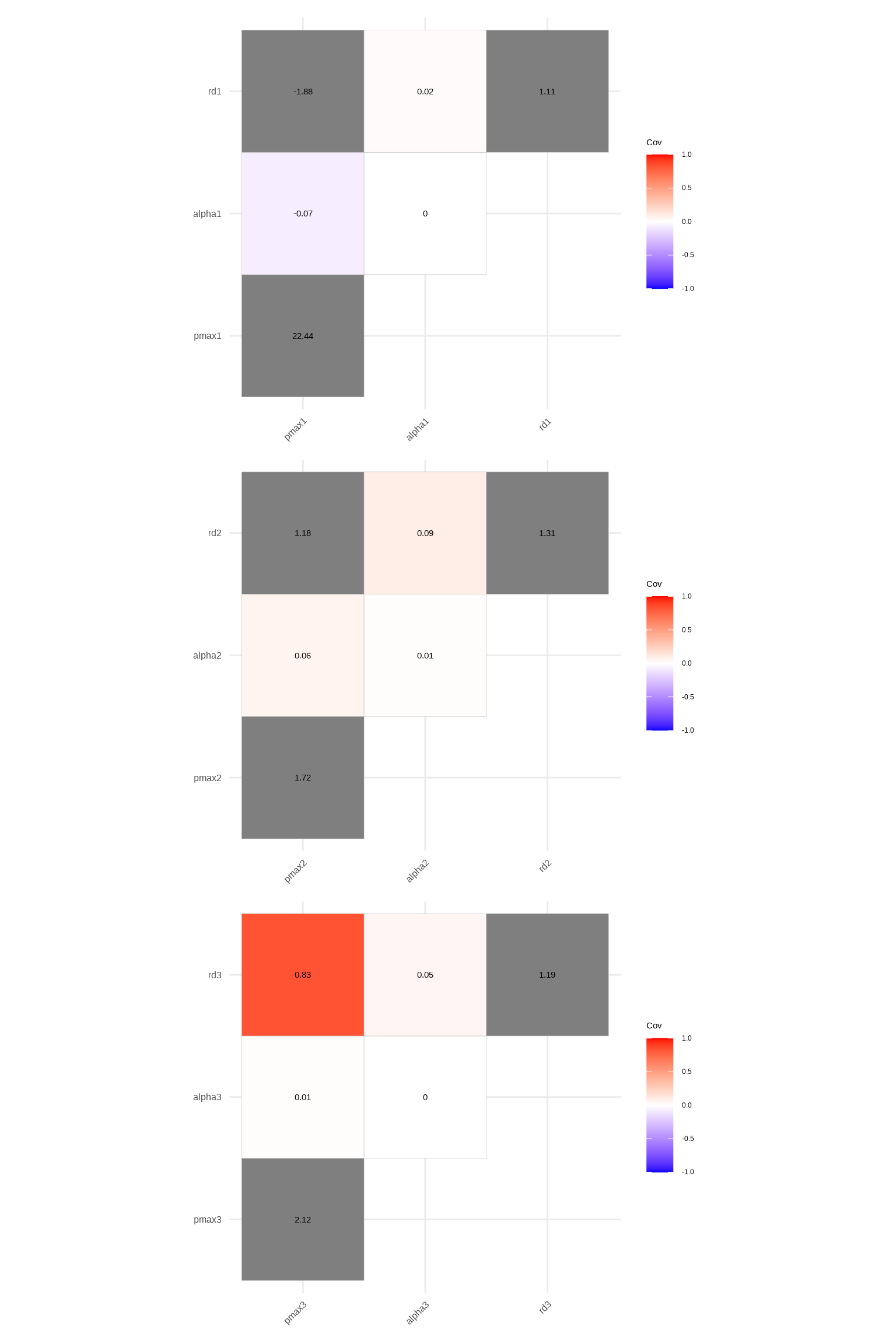

モデル係数はお互いに独立していないことが明確ですね。これにより、Wald’s 検定の結果はそのまま受け入れないほうがいいです。

11.8 ガウス誤差伝播法

ガウス誤差伝播法 (Gaussian error propagation, GEP) は直接推定したパラメータ（係数）から間接的に求めたパラメータの誤差を推定するための手法です。 GEP においては、誤差が正規分布に従うことと、パラメータ推定にバイアスがないことが条件です。ところがほとんどのモデルは、この条件を満たしていません。それにしても、推定した誤差がパラメータ期待値の 10% を下回れば、信頼できる結果と考えられます。

GEPを実施するには、つぎの式を応用します。 \(\sigma_f^2\) は間接的に求めたパラメータ \(f\) の分散です。 \(g\) は間接的に求めたパラメータ \(f\) の偏微分方程式の行列です。 \(V\) は直接推定したパラメータの分散共分散行列です。

\[ \sigma_f^2 = \mathbf{g}^T\mathbf{V}\mathbf{g} \] \[ \mathbf{g} = \begin{bmatrix} \frac{\partial f}{\partial \beta_x}\\ \frac{\partial f}{\partial \beta_y}\\ \frac{\partial f}{\partial \beta_z}\\ \end{bmatrix} \]

\[ \mathbf{V} = \begin{bmatrix} \sigma_{xx}^2 & \sigma_{xy}^2 & \sigma_{xz}^2 \\ \sigma_{xy}^2 & \sigma_{yy}^2 & \sigma_{yz}^2 \\ \sigma_{xz}^2 & \sigma_{yz}^2 & \sigma_{zz}^2 \\ \end{bmatrix} \]

\[ \sigma_f^2 = \begin{bmatrix} \frac{\partial f}{\partial \beta_x}& \frac{\partial f}{\partial \beta_y}& \frac{\partial f}{\partial \beta_z}\\ \end{bmatrix} \begin{bmatrix} \sigma_{xx}^2 & \sigma_{xy}^2 & \sigma_{xz}^2 \\ \sigma_{xy}^2 & \sigma_{yy}^2 & \sigma_{yz}^2 \\ \sigma_{xz}^2 & \sigma_{yz}^2 & \sigma_{zz}^2 \\ \end{bmatrix} \begin{bmatrix} \frac{\partial f}{\partial \beta_x}\\ \frac{\partial f}{\partial \beta_y}\\ \frac{\partial f}{\partial \beta_z}\\ \end{bmatrix} \]

\[ \begin{aligned} \sigma_f^2 &= \frac{\partial f}{\partial \beta_x}\left(\frac{\partial f}{\partial \beta_x}\sigma_{xx}^2 +\frac{\partial f}{\partial \beta_y}\sigma_{xy}^2 +\frac{\partial f}{\partial \beta_z}\sigma_{xz}^2\right) \\ {} &+ \frac{\partial f}{\partial \beta_y}\left(\frac{\partial f}{\partial \beta_x}\sigma_{xy}^2 +\frac{\partial f}{\partial \beta_y}\sigma_{yy}^2 +\frac{\partial f}{\partial \beta_z}\sigma_{yz}^2\right) \\ {} &+ \frac{\partial f}{\partial \beta_z}\left(\frac{\partial f}{\partial \beta_x}\sigma_{xz}^2 +\frac{\partial f}{\partial \beta_y}\sigma_{yz}^2 +\frac{\partial f}{\partial \beta_z}\sigma_{zz}^2\right) \end{aligned} \]

\[ \begin{aligned} \sigma_f^2 &= \left(\frac{\partial f}{\partial \beta_x}\right)^2\sigma_{xx}^2 + \frac{\partial f}{\partial \beta_x}\frac{\partial f}{\partial \beta_y}\sigma_{xy}^2 + \frac{\partial f}{\partial \beta_x}\frac{\partial f}{\partial \beta_z}\sigma_{xz}^2 \\ {} & + \left(\frac{\partial f}{\partial \beta_y}\right)^2\sigma_{yy}^2 + \frac{\partial f}{\partial \beta_y}\frac{\partial f}{\partial \beta_x}\sigma_{xy}^2 + \frac{\partial f}{\partial \beta_y}\frac{\partial f}{\partial \beta_z}\sigma_{yz}^2 \\ {} &+ \left(\frac{\partial f}{\partial \beta_z}\right)^2\sigma_{zz}^2 + \frac{\partial f}{\partial \beta_z}\frac{\partial f}{\partial \beta_x}\sigma_{xz}^2 + \frac{\partial f}{\partial \beta_z}\frac{\partial f}{\partial \beta_y}\sigma_{yz}^2 \end{aligned} \]

\[ \begin{aligned} \sigma_f^2 &= \left(\frac{\partial f}{\partial \beta_x}\right)^2\sigma_{xx}^2 + \left(\frac{\partial f}{\partial \beta_y}\right)^2\sigma_{yy}^2 + \left(\frac{\partial f}{\partial \beta_z}\right)^2\sigma_{zz}^2 \\ {} &+ 2\left(\frac{\partial f}{\partial \beta_x}\frac{\partial f}{\partial \beta_y}\sigma_{xy}^2 + \frac{\partial f}{\partial \beta_x}\frac{\partial f}{\partial \beta_z}\sigma_{xz}^2 + \frac{\partial f}{\partial \beta_y}\frac{\partial f}{\partial \beta_z}\sigma_{yz}^2 \right) \end{aligned} \]

参考文献：

Tellinghuisen J. 2000. Statistical error propagation. Journal of Physical Chemistry A 104: 2834 - 2844.
Tellinghuisen J. 2001. Statistical error propagation. Journal of Physical Chemistry A 105: 3917 - 3921.
Lo E. 2005. Gaussian error propagation applied to ecological data: Post-ice-storm-downed woody biomass. Ecological Monographs 75: 451-466.

\[ \sigma_f^2=\sum_{i = 1}^n \left(\frac{\partial q}{\partial x_i}\sigma_{x_i}\right)^2 + 2\sum_{i = 1}^n\sum_{j = 1,j\neq i}^n \left(\frac{\partial q}{\partial x_i}\frac{\partial q}{\partial x_j}\rho_{x_i x_j}\sigma_{x_i}\sigma_{x_j}\right) \]

共分散と相関の関係は次の通りです。

\[ \overbrace{\rho_{xy}}^\text{相関}= \overbrace{\sigma_{xy}}^\text{共分散} / \underbrace{(\sigma_x\sigma_y)}_{x,y\;\text{の標準偏差}} \]

では、Rで解析に使ったモデルの偏微分方程式を求めます。光飽和点 \((I_k)\) と光補償点 \((I_c)\) の formula は次のように定義します。

\[ \begin{aligned} I_k & = f_1 = P_{max} / \alpha \\ I_c & = f_2 = \frac{P_{max}}{\alpha} \ln\left(\frac{P_{max}}{P_{max} - R_d}\right) \\ \end{aligned} \]

fic = ic ~ pmax/alpha
fik = ik ~ pmax/alpha * log(pmax/(pmax - rd))

fic と fik は 3つの要素で組み立てられた formula です。たとえば、ficの場合は次のようになっています。

class(fic)
#> [1] "formula"
length(fic)
#> [1] 3
fic[[1]]
#> `~`
fic[[2]]
#> ic
fic[[3]]
#> pmax/alpha

それぞれの偏微分方程式は次のとおりになります。

光補償点 \((f_1)\) の場合、 \(P_{max}\) と \(\alpha\) に対する式は次のとおりです。

\[ \begin{aligned} \frac{\partial f_1}{\partial \alpha} &= \frac{-P_{max}}{\alpha^2} \\ \frac{\partial f_1}{\partial P_{max}} &= \frac{1}{\alpha} \\ \end{aligned} \]

光飽和点 \((f_2)\) の場合、\(R_d\)　もあるので式は次のとおりです。

\[ \begin{aligned} \frac{\partial f_2}{\partial \alpha} &= -\frac{P_{max}}{\alpha^2} \log\left(\frac{P_{max}}{P_{max} - R_d}\right) \\ \frac{\partial f_2}{\partial P_{max}} &= \frac{1}{\alpha} \log\left(\frac{P_{max}}{P_{max} - R_d}\right) + \left(\frac{1}{\alpha} - \frac{P_{max}}{P_{max}-R_d}\right) \\ \frac{\partial f_2}{\partial R_{d}} &= \frac{P_{max}}{\alpha\,(P_{max}-R_d)} \\ \end{aligned} \] Rでは、次の関数をつかって、光合成光曲線の光補償点と光飽和点の誤差を求めます。関数に rlang パッケージの関数をつかています。

propagate_error = function(model, dmodel, parameters) {
  require(rlang)  
  cfs = coefficients(model)    # モデル係数の期待値
  vars = all.vars(dmodel[[3]]) # 偏微分方程式の対象となる変数
  V = vcov(model)              # 当てはめたモデルの分散共分散行列
  
  V = V[parameters, parameters] # 必要な分散共分散の抽出
  expectation = cfs[parameters] # 必要な期待値の抽出
  
  # 偏微分方程式はここで求めています。
  gradient_fn = deriv(dmodel[[3]], vars, function.arg = T)
  ff = expr(gradient_fn(!!!syms(vars)))
  tmp =  exprs(!!!expectation)
  tmp = set_names(tmp, vars)
    for(i in 1:length(vars)) {
    call2("=", expr(!!vars[i]), expectation[i]) |> eval()
  }
  G = eval(ff)
  G = attributes(G)$gradient |> matrix(ncol = 1)
  
  # g^T V g
  sqrt((t(G) %*% V) %*% G)
}

直接推定したモデル係数を抽出して、期待値と標準誤差だけ残します。

cfsout = summary(fullmodel)$coef |> as_tibble(rownames = "parameter") |> 
  select(parameter, est=Estimate, se = `Std. Error`) |> 
  mutate(id = str_extract(parameter, "[0-9]"),
         parameter = str_extract(parameter, "[A-z]+")) |> 
  pivot_wider(names_from = parameter,
              values_from = c(est, se),
              names_glue = "{.value}_{parameter}")

間接的に推定したパラメータを追加します。

cnames = c("Seaweed", "Parameter", "Estimate", "SE")
cfsout = cfsout |> 
  mutate(est_ic = est_pmax / est_alpha,
         est_ik = est_pmax / est_alpha * log(est_pmax / (est_pmax - est_rd))) |> 
  mutate(pmax = str_c("pmax", id),
         alpha = str_c("alpha", id),
         rd = str_c("rd", id),
         seaweed = c("ウミトラノオ", "コブクロモク", "幼体"))

propagate_error() をそれぞれの海藻に適応します。

apply_propagate_error_fic = function(pmax, alpha, rd) {
    fic = ic ~ pmax / alpha
    propagate_error(fullmodel, fic, c(pmax, alpha))
}

apply_propagate_error_fik = function(pmax, alpha, rd) {
  fik = ik ~ pmax / alpha * log(pmax / (pmax - rd))
    propagate_error(fullmodel, fik, c(pmax, alpha, rd))
}

cfsout = cfsout |> 
  mutate(se_ic = pmap_dbl(list(pmax, alpha, rd), apply_propagate_error_fic)) |> 
  mutate(se_ik = pmap_dbl(list(pmax, alpha, rd), apply_propagate_error_fik)) |> 
           select(-alpha, -pmax, -rd) |> 
  pivot_longer(cols = matches("est_|se_"),
               names_to = c("stat", "par"),
               names_pattern = "(est|se)_(.*)") |> 
  pivot_wider(names_from = stat, values_from = value) |> 
  arrange(par, id) |> 
  select(-id)

cfsout |> 
  kableExtra::kbl(digits = c(0,0,3,2),
                  col.names = cnames)

Seaweed	Parameter	Estimate	SE
ウミトラノオ	alpha	0.086	0.02
コブクロモク	alpha	0.165	0.10
幼体	alpha	0.072	0.05
ウミトラノオ	ic	271.401	109.63
コブクロモク	ic	31.837	17.59
幼体	ic	62.725	49.15
ウミトラノオ	ik	25.353	9.00
コブクロモク	ik	2.735	6.34
幼体	ik	12.739	11.54
ウミトラノオ	pmax	23.286	4.74
コブクロモク	pmax	5.241	1.31
幼体	pmax	4.501	1.46
ウミトラノオ	rd	2.077	1.05
コブクロモク	rd	0.432	1.14
幼体	rd	0.827	1.09

10 モデル選択

12 ggplot