15 冗長性分析 (RDA)
冗長性分析は多変量解析 (multivariate analysis) の一種です。 多変量解析の目的は多変量・多次元の応答変数 (response variable, observation) の特徴を要約または予測することです。 重回帰分析、主成分分析、クラスター分析、多次元尺度更生法は代表的な方法です。
多変量解析の中に、座標づけ・順序づけ (ordination) を用いる解析方法があります。 これは、多次元の説明変数と多次元の応答変数 (explanatory variable, predictor) の多変量解析です。 もっと簡易に説明すると、多変量解析は unconstrained と constrained に分けられます。
では、冗長性分析は群集生態学の解析に用いる手法の 1 つです。 実際には主成分分析を説明変数で constrained したものが冗長性分析です。 例えば、種の行列データが応答変数となり、温度や風速、降水量などの環境要因の行列データが説明変数となります。 つまり、生物群集と環境変数の関係を調べられます。
冗長性分析をするなら、解析するまえに次の作業が必要です。
- 応答変数の単位が異なる場合、データのスケールが同じになるようにしてください。説明変数の z 値を求めることが一般的ですが、カウントのデータはそのまま使いましょう。
- 説明変数の数はサンプル・観測値・サイトの数より少ないようにすること。
- 説明変数の単位が異なる場合、応答変数と同じように z 値を求めてください。
- 各説明変数と各応答変数のペアの関係が直線であることを確認してください。直線はない場合は、変数の変換を検討してください。
- ユークリッド距離以外の距離を使用するなら、生態学に適切な変換を使ってください。へリンガ変換 (Hellinger transform) は種数に適しています。へリンガ変換はゼロや少数の重み付けは低いです。
15.2 データの読み込み
地点の緯度、経度、地点名のデータを読み込みます。
# 地点のデータ.
mogi = tibble(long = 129.9153635749726, lat = 32.70623687738632, spot = "茂木港")
hachikoku = tibble(long = 129.8383693424696, lat = 32.84731449061039, spot = "時津八工区")
shinnagasaki = tibble(long = 129.76273726531167, lat = 32.81348550319948, spot = "新長崎漁港")
iojima = tibble(long = 129.7821657616903, lat = 32.703793584891876, spot = "伊王島")
makishima = tibble(long = 129.965811722672, lat = 32.75280526296073, spot = "牧島弁天")
uki = tibble(long = 130.08539712666882, lat = 32.79186359942752, spot = "有喜")
chijiwa = tibble(long = 130.18963213745377, lat = 32.78110330164613, spot = "千々石")
nagasakigyoko = tibble(long = 129.8655064038331, lat = 32.74467008358571, spot = "長崎港")
oseto = tibble(long = 129.63277961757416, lat = 32.93102986237914, spot = "大瀬戸地磯")
yuinohama = tibble(long = 129.99744215828974, lat = 32.75999373754844, spot = "結の浜")
nagayo = tibble(long = 129.865934845824, lat = 32.84614488892818, spot = "長与")
koe = tibble(long = 129.81160493756988, lat = 32.75672238458309, spot = "小江港")
kaminoshima = tibble(long = 129.8195940446883, lat = 32.72418777847413, spot = "神の島")
nanakoku = tibble(long = 129.84686360804426, lat = 32.83951168442669, spot = "時津七工区")
togitsuko = tibble(long = 129.84779161587724, lat = 32.83386270229517, spot = "時津港")
tameshi = tibble(long = 129.84086842907925, lat = 32.63768592814823, spot = "為石港")
maria = tibble(long = 129.82697052559877, lat = 32.71645046633131, spot = "神の島(マリア像)")
kabashima = tibble(long = 129.78207587005704, lat = 32.56964417259288, spot = "樺島")
wakimisaki = tibble(long = 129.7844175224698, lat = 32.57935098714508, spot = "脇岬港")
takashima = tibble(long = 129.75940675600606, lat = 32.6701574982406, spot = "高島釣り公園")
fukahori = tibble(long = 129.81655615391824, lat = 32.684034723520824, spot = "深堀")
ainoura = tibble(long = 129.65998414190727, lat = 33.17044115356162, spot = "相浦川")
odo = tibble(long = 129.80164858578118, lat = 32.91795820807477, spot = "尾戸")
enoura = tibble(long = 130.03532906360107, lat = 32.76477883221611, spot = "江の浦漁港")
fukushima = tibble(long = 129.82510401615977, lat = 33.361672678116534, spot = "福島")
kisashi = tibble(long = 130.19682599039155, lat = 32.71797951737513, spot = "木指")
ikeshimo = tibble(long = 129.98698524182933, lat = 32.757089717364224, spot = "池下")
kidu = tibble(long = 130.1877412283317, lat = 32.76624792288015, spot = "木津")
kunisaki = tibble(long = 130.13379349135502, lat = 32.6835771032792, spot = "国﨑半島")
yokose = tibble(long = 129.70488196433504, lat = 33.08595494898572, spot = "横瀬港")
sasebogawa = tibble(long = 129.72194554448632, lat = 33.16169028908325, spot = "佐世保川河口")
mie = tibble(long = 129.74786663770905, lat = 32.820159276236936, spot = "三重漁港")
nagushi = tibble(long = 130.1424470044555, lat = 32.681644023378894, spot = "南串(京泊)")
shishigawa = tibble(long = 129.80598029708491, lat = 32.86486310040935, spot = "子々川")
obama = tibble(long = 130.2055019801174, lat = 32.73220809832507, spot = "小浜")
tobiko = tibble(long = 130.1668200832182, lat = 32.697084316063425, spot = "飛子")
aba = tibble(long = 129.94851786984017, lat = 32.755822723429574, spot = "網場")
nezumishima = tibble(long = 129.83509963298388, lat = 32.7200235294155, spot = "神の島(鼠島)")
sakito = tibble(long = 129.64031098930263, lat = 33.041195585109726, spot = "崎戸大島")
higashihama = tibble(long = 129.7434881947802, lat = 33.133498396367585, spot = "東浜港")
higashiookawa = tibble(long = 130.00122186927044, lat = 32.84251398315686, spot = "東大川")
kadusa = tibble(long = 130.16169860577867, lat = 32.62263363021445, spot = "加津佐漁港")
spot_info =
bind_rows(mogi, hachikoku, shinnagasaki, iojima, makishima, uki, chijiwa, nagasakigyoko,
oseto, yuinohama, nagayo, koe, kaminoshima, nanakoku, togitsuko, tameshi,
maria, kabashima, wakimisaki, takashima, fukahori, ainoura, odo,
enoura, fukushima, kisashi, ikeshimo, kidu, kunisaki, yokose, sasebogawa,
mie, nagushi, shishigawa, obama, tobiko, aba, nezumishima, sakito,
higashihama, higashiookawa, kadusa)次に、釣果のデータを読み込みます。 ネット上から集めたデータなので, 記入ミスや測定方法の違いがあります. 文字列処理を行って, データを丁寧に整形していきます。
釣果データを読み込みます。 データは研究室サーバにあります。
tanimaesfolder = "~/Lab_Data/tanimaes/share_files/example_data/"
filename = "nagasaki_fishing_spot_fishdata.rds"
fish_data0 = str_c(tanimaesfolder, filename) |> read_rds()case_when() を使って、和名を整えます。
fish_data1 = fish_data0 |>
unnest(data) |>
mutate(species_j = case_when(
str_detect(species_j, "^アジゴ?$") ~ "マアジ",
str_detect(species_j, "^アラカブ+") ~ "カサゴ",
str_detect(species_j, "エギング") ~ "アオリイカ",
str_detect(species_j, "^クロ$") ~ "メジナ",
str_detect(species_j, "^サゴシ$") ~ "サワラ",
str_detect(species_j, "^サバゴ?$") ~ "サバ",
str_detect(species_j, "シーバス|セイゴ") ~ "スズキ",
str_detect(species_j, "^チヌ$") ~ "クロダイ",
str_detect(species_j, "^ネリゴ$") ~ "カンパチ",
str_detect(species_j, "^ハタ$") ~ "キジハタ",
str_detect(species_j, "ハマチ|ヤズ|ブリ") ~ "ブリ",
str_detect(species_j, "^ヒラス$") ~ "ヒラマサ",
str_detect(species_j, "^タコ$") ~ "マダコ",
str_detect(species_j, "^メッキアジ$") ~ "メッキ",
str_detect(species_j, "^メバリング$") ~ "メバル",
str_detect(species_j, "^モンゴウイカ$") ~ "カミナリイカ",
str_detect(species_j, "^太刀魚$") ~ "タチウオ",
str_detect(species_j, "^真鯛$") ~ "マダイ",
str_detect(species_j, "^キス$") ~ "シロギス"
))species_j が 木指または size が 1杯のデータを外す。
fish_data1 = fish_data1 |>
filter(!str_detect(species_j, "木指")) |>
filter(!str_detect(size, "1杯"))stringi パッケージの stri_trans_nfkd() 関数を使って、全角を半角に変換する。
すの次に、size と weight の情報を 1 列にまとめる。
fish_data1 = fish_data1 |>
mutate(size = stri_trans_nfkd(size)) |>
mutate(weight = stri_trans_nfkd(weight)) |>
mutate(date = ymd(date)) |>
mutate(size = ifelse(is.na(size), weight, size))size 変数をさらに整える。
fish_data2 = fish_data1 |>
mutate(size = ifelse(str_detect(size, pattern = "手|掌"), "20cm", size), # 「手のひら」は 20cm と定義.
size = ifelse(str_detect(size, pattern = "コロッケ"), "10cm", size), # 「コロッケサイズ」は 10cm と定義.
size = str_replace(size, pattern = "三", replacement = "3"),
size = str_replace(size, pattern = "四", replacement = "4"),
size = str_replace(size, pattern = "本半", replacement = ".5")) # 漢数字をアラビア数字に.
fish_data2 = fish_data2 |>
mutate(type = ifelse(str_detect(size, pattern = "[Cc]?[Mm㎝]|センチ"), "length", "width")) |> # 評価基準.
mutate(type = ifelse(str_detect(size, pattern = "[Kk]?[Gg㎏ℊ]|キロ"), "weight", type)) |> # 評価基準.
mutate(size = str_remove(size, pattern = ".*[~∼]")) |> # チルダ記号より前の文字列を消去.
mutate(size = as.double(str_extract(size, pattern = "[0-9,.]+"))) |> # サイズの数値部分のみ抽出.
mutate(type = ifelse(type == "width" & size > 180, "weight", type), # 重量っぽいものを重量評価に.
type = ifelse(type == "width" & between(size, 9, 180), "length", type)) |> # 長さっぽいものを長さ評価に.
mutate(size = ifelse(type == "weight" & size < 30, size*1000, size)) |> # キロっぽいものはグラム評価に.
select(spot, long, lat, date, species_j, type, size, method) |>
drop_na()次は、長さ, 重さ, 幅 の値を標準化します。 10cm, 20cm, 30cm, 1kg, 2kg, 3kg のアオリイカを, 数値で並び替えると Max:30 , Min:1 となってしまうので、測定方法ごとにグループ化し, 正規化します。 正規化された値に 10 をかけて 50 を足すと, 学力偏差値でお馴染みの偏差値になります。
fish_data2 = fish_data2 |>
group_by(type) |>
mutate(size_scl = scale(log(size))[,1]) |>
ungroup()
fish_data2
#> # A tibble: 565 × 9
#> spot long lat date species_j type size method
#> <chr> <dbl> <dbl> <date> <chr> <chr> <dbl> <chr>
#> 1 茂木… 130. 32.7 2022-04-29 シロギス leng… 25 投げ…
#> 2 茂木… 130. 32.7 2022-04-27 シロギス leng… 15 投げ…
#> 3 茂木… 130. 32.7 2022-03-17 シロギス leng… 15 投げ…
#> 4 茂木… 130. 32.7 2022-03-03 メジナ leng… 25 フカ…
#> 5 茂木… 130. 32.7 2022-01-22 シロギス leng… 21 投げ…
#> 6 茂木… 130. 32.7 2022-01-07 カサゴ leng… 20 ブラ…
#> 7 茂木… 130. 32.7 2021-12-09 シロギス leng… 23 投げ…
#> 8 茂木… 130. 32.7 2021-11-29 ブリ leng… 60 ルアー
#> 9 茂木… 130. 32.7 2021-11-15 マアジ leng… 25 サビ…
#> 10 茂木… 130. 32.7 2021-11-08 マアジ leng… 20 サビ…
#> # … with 555 more rows, and 1 more variable: size_scl <dbl>釣果のデータを整形し終わりました。 うまく整形できているか、可視化することで確認してみます。
# 作図.
p1 = fish_data2 |>
ggplot() +
geom_jitter(aes(reorder(species_j, size_scl), size_scl, color = type),
width = 0.1) +
scale_color_viridis_d(end = 0.8) +
theme(axis.text.x = element_text(angle = 45, hjust = 1, vjust = 1))
p2 = fish_data2 |>
mutate(month = month(date)) |>
ggplot() +
geom_point(aes(month, size_scl)) +
scale_x_continuous(breaks = 1:12) +
facet_wrap("species_j")
p1 + p2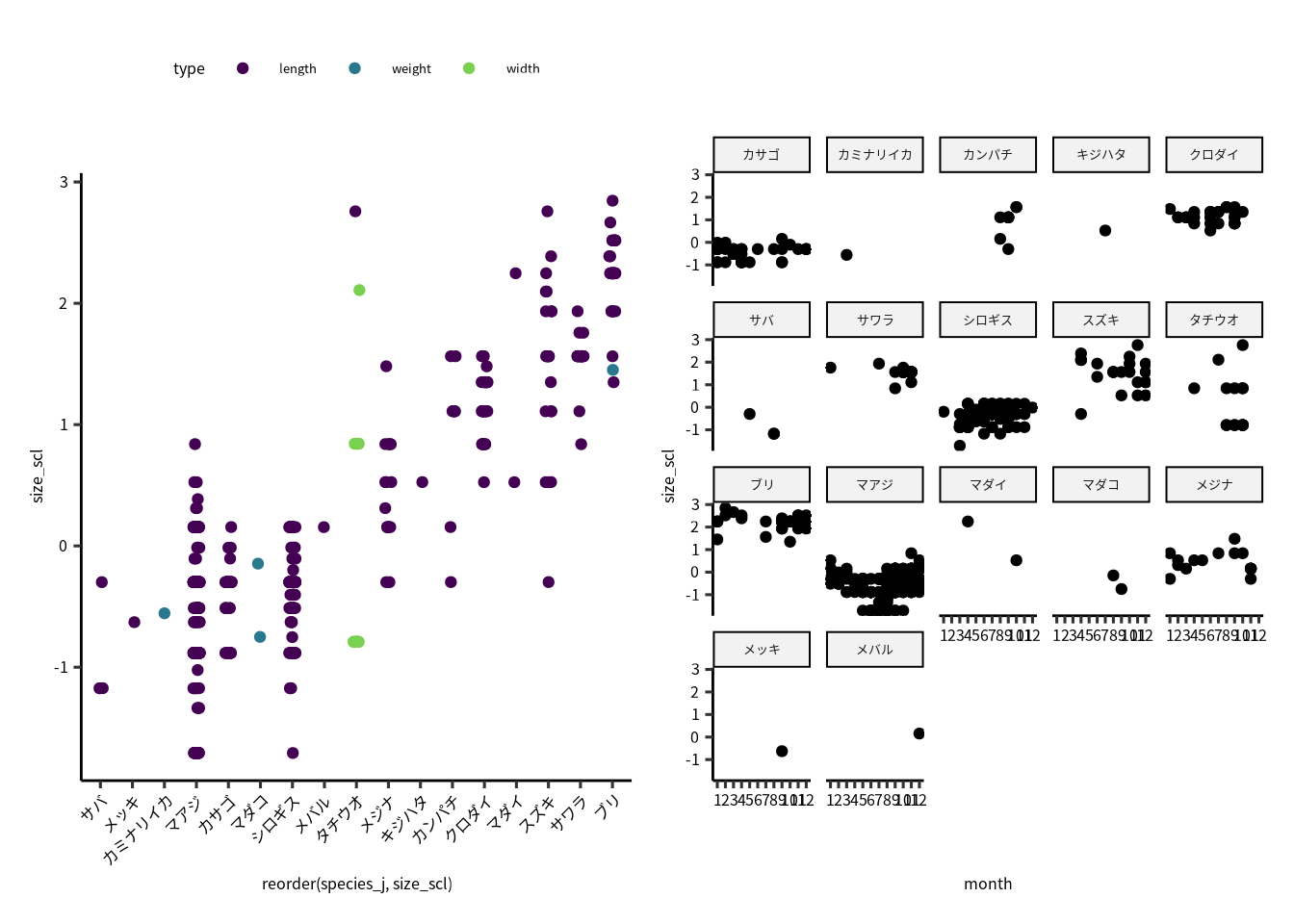
種組成の類似度を説明する環境要因のデータを用意します。
# その他の変数.
# 種. これは分析に用いませんが ggplot 用に作っておきます.
sp_info = fish_data2 |>
group_by(spot) |>
summarise(n = length(species_j),
max_size = max(size_scl),
mean_size = mean(size_scl))
# fetch. (送風距離)
filename = "nagasaki_fishing_spot_fetch.rds"
fetch_info = str_c(tanimaesfolder, filename) |> read_rds()
fetch_info = fetch_info |>
unnest(length) |>
group_by(spot) |>
summarise(mean_f = mean(length, na.rm = T), .groups = "drop")15.3 GIS の処理
GIS用の tibble(地図用のデータ)は sf パッケージの st_as_sf() で作ります。
spot_info を EPSG:4326 (WGS84) の座標参照系に設定します。
suisa_gps も同じように作ります。
spot_gps = spot_info |>
st_as_sf(coords = c("long", "lat"), crs = st_crs(4326), agr = "constant")
suisan_gps = tibble(spot = "水産学部",
long = 129.86544761304938, lat = 32.786294986775076) |>
st_as_sf(coords = c("long", "lat"), crs = st_crs(4326), agr = "constant")距離を求めるためには、座標参照系を EPSG:2450 (JDG2000, 日本座標系) に変換します。 緯度経度は東距 (northing) と北距 easting((単位はメートル)に代わります。
spot_gps = spot_gps |> st_transform(st_crs(2450))
suisan_gps = suisan_gps |> st_transform(st_crs(2450))
std = st_distance(spot_gps, suisan_gps) |> as.vector()
spot_info = spot_info |> mutate(dist_from_sui = std)
spot_info
#> # A tibble: 42 × 4
#> long lat spot dist_from_sui
#> <dbl> <dbl> <chr> <dbl>
#> 1 130. 32.7 茂木港 10115.
#> 2 130. 32.8 時津八工区 7285.
#> 3 130. 32.8 新長崎漁港 10163.
#> 4 130. 32.7 伊王島 12124.
#> 5 130. 32.8 牧島弁天 10190.
#> 6 130. 32.8 有喜 20774.
#> 7 130. 32.8 千々石 30609.
#> 8 130. 32.7 長崎港 4653.
#> 9 130. 32.9 大瀬戸地磯 27276.
#> 10 130. 32.8 結の浜 12806.
#> # … with 32 more rowsXMLデータから河川の位置情報を読み込みます。
filename = "W05-07_42.xml"
tanimaesxmlfolder = "~/Lab_Data/tanimaes/seaweed_data/info/"
river = str_c(tanimaesxmlfolder, filename) |> read_xml()
river = river |>
html_elements(xpath = '///GM_PointArray.column') |>
xml_children() |>
xml_text() |>
as_tibble()読み込んだあと、河川の識別をします。
river = river |>
mutate(value = ifelse(value == "", "river_sep", value)) |>
mutate(river_id = ifelse(str_detect(value, pattern = "river_sep"), 0.5, 0)) |>
mutate(river_id = cumsum(river_id) + 0.5) |>
filter(value != "river_sep") |>
separate(value, into = c("lat", "long"), sep = " ") |>
mutate(across(c("lat", "long"), ~ as.double(.x)))ここで sf オブジェクトに変換します。
Region of interest (ROI, 関心領域) に河川データを絞ります。
river_boundary = st_bbox(c(xmin = 129.5, xmax = 130,
ymin = 32.5, ymax = 33.1), crs = st_crs(4326))
river_boundary = river_boundary |> st_as_sfc()
river = st_crop(river, river_boundary)
river = river |>
group_by(river_id) |>
mutate(n = row_number()) |>
mutate(status = ifelse(n == max(n), T, F)) 河口と川の合流地点に色を付けます。
ggplot(river) +
geom_sf(aes(color = status)) +
scale_color_viridis_d("河口域")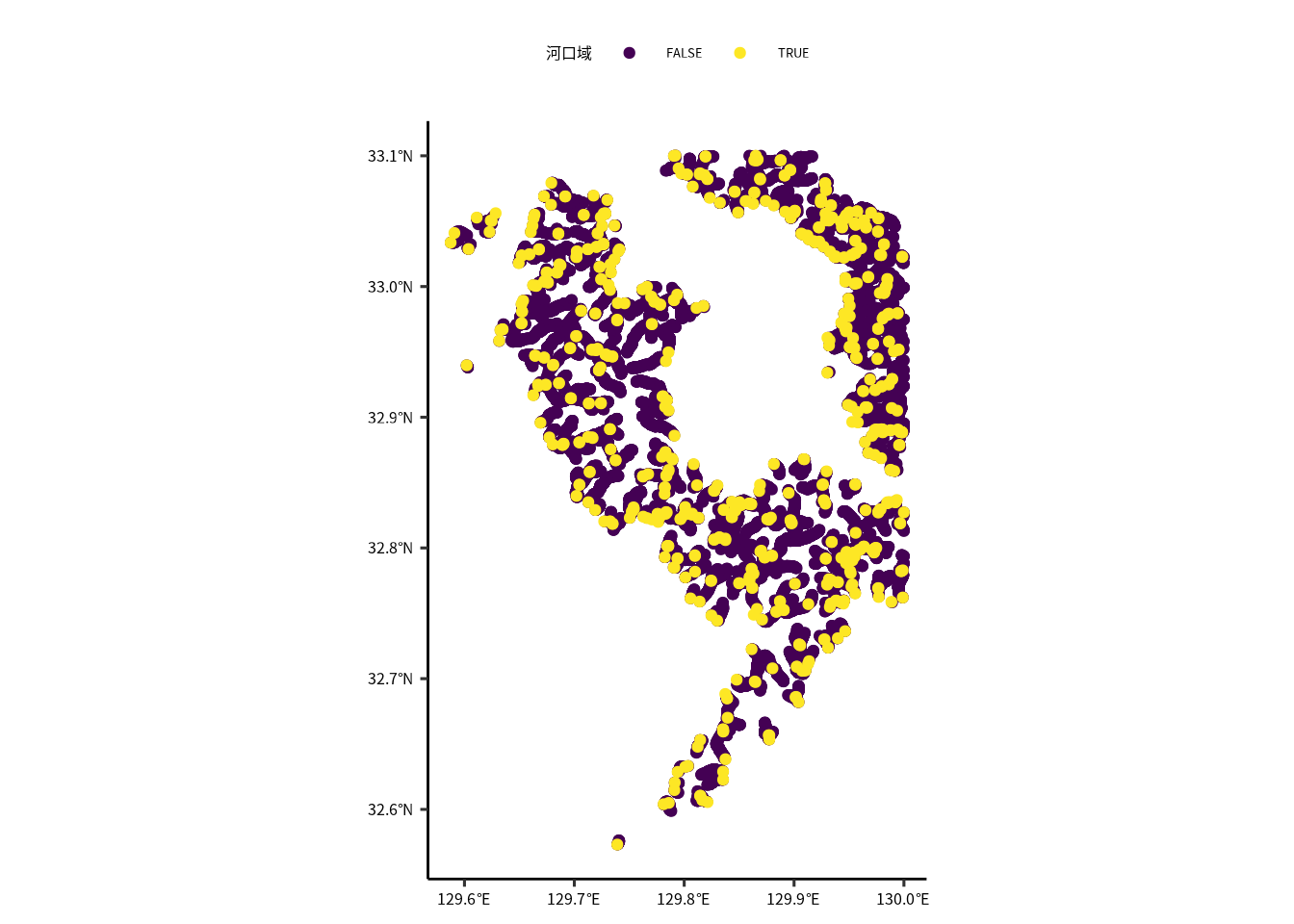
Figure 11.1: 河川の河口域を特定して、色で区別しました。
spot_gps の位置と河口域の距離を求めます。
river から河口域の位置情報を抽出します。
river_mouth_info の座標参照系を EPSG:2450 に変換します。
river_mouth_gps = river_mouth_info |> st_transform(st_crs(2450))st_distance() 関数を使って、river_mouth_gps と spot_gps の距離を求めます。
結果は n x m の行列です。
長崎大学水産学部からの距離は、ここで再計算しています。
最後の mutate() は距離を m から km に変換しています。
calc_distance_nearest_river_mouth = function(data, origin) {
st_distance(origin, data) |> as_vector() |> min()
}
river_mouth_info = spot_gps |>
group_nest(spot) |>
mutate(dist_from_river =
map_dbl(data, calc_distance_nearest_river_mouth,
origin = river_mouth_gps)) |>
mutate(dist_from_suisan =
map_dbl(data, calc_distance_nearest_river_mouth,
origin = suisan_gps)) |>
mutate(across(starts_with("dist"), ~ . / 1000)) |>
unnest(data)上の処理をすると、座標参照系の情報が消えたので、ここで再び付けます。
river_mouth_info = river_mouth_info |> st_as_sf(crs = st_crs(2450))
river_mouth_info
#> Simple feature collection with 42 features and 3 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -820809.1 ymin: -318563.7 xmax: -820809.1 ymax: -318563.7
#> Projected CRS: JGD2000 / Japan Plane Rectangular CS VIII
#> # A tibble: 42 × 4
#> spot geometry dist_from_river
#> * <chr> <POINT [m]> <dbl>
#> 1 三重漁港 (-820809.1 -318563.7) 0.403
#> 2 伊王島 (-818658.1 -331798.2) 5.50
#> 3 佐世保川河口 (-820048 -280305.1) 9.46
#> 4 加津佐漁港 (-783625.6 -343734.2) 21.9
#> 5 千々石 (-779599.8 -326292.3) 18.0
#> 6 南串(京泊) (-784919.2 -337018) 16.3
#> 7 国﨑半島 (-785717.3 -336737.9) 15.5
#> 8 大瀬戸地磯 (-830591.3 -305298.9) 3.06
#> 9 子々川 (-814928.6 -314037.7) 0.265
#> 10 小江港 (-815397.5 -326130.3) 0.341
#> # … with 32 more rows, and 1 more variable:
#> # dist_from_suisan <dbl>15.4 冗長性分析 (RDA)
RDA などの序列化に用いるデータは横長にする必要があります。
つまり、列の並びは(説明変数1、説明変数2、説明変数3、生物種1、生物種2、生物種3…)
のようにしなければなりません。
そこで一旦、生物の行列と説明変数の tibble に分けて整形します。
また、地点ごとに釣果データの数が異なるので、生物の行列データについてへリンガー変換を実施します。
RDA 用のデータを組み立てます。
応答変数の種構成行列は fish_data2 から作ります。
まずは、spot と species_j 毎の総数を求めます。
Y = fish_data2 |>
group_by(spot, species_j) |>
summarise(n = n(), .groups = "drop") |>
pivot_wider(names_from = species_j, values_from = n, values_fill = 0)こんど、説明変数の tibble を準備します。
X = left_join(fetch_info, river_mouth_info, by = "spot")spot 毎の種数を求めます。
species_n = Y |> pivot_longer(-spot) |>
group_by(spot) |>
summarise(n = sum(value > 0))
X = inner_join(X, species_n)fetch_info と river_mouth_info を結合したら、説明変数を正規化します.
scale_data = function(x) {
scale(x) [, 1]
}
X = X |> mutate(across(c(mean_f, matches("dist")), scale_data))Y に存在しない X の情報を確認します。
anti_join(X, Y)
#> # A tibble: 0 × 6
#> # … with 6 variables: spot <chr>, mean_f <dbl>,
#> # geometry <GEOMETRY [m]>, dist_from_river <dbl>,
#> # dist_from_suisan <dbl>, n <int>データが合わないので、ここで修正します。
X = semi_join(X, Y)最後に、X と Y の行の順序を合わせます。
では、種構成行列の仕上げです。
つぎに、種構成行列をへリンガ変換 (Hellinger transformation) します。
Y = decostand(Y, method = "hellinger")モデルを記述します。 今回は、地点間の類似性を説明する説明変数がそもそも少ないです。
# モデル選択.
r1 = rda(Y ~ dist_from_river, data = X)
r2 = rda(Y ~ mean_f, data = X)
r3 = rda(Y ~ dist_from_suisan, data = X)
anova(r1, by = "terms", permutations = 999) # 変数ごとに P 値を確認.
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = Y ~ dist_from_river, data = X)
#> Df Variance F Pr(>F)
#> dist_from_river 1 0.01771 1.2087 0.28
#> Residual 38 0.55676
anova(r2, by = "terms", permutations = 999) # 変数ごとに P 値を確認.
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = Y ~ mean_f, data = X)
#> Df Variance F Pr(>F)
#> mean_f 1 0.02458 1.6984 0.123
#> Residual 38 0.54989
anova(r3, by = "terms", permutations = 999) # 変数ごとに P 値を確認.
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = Y ~ dist_from_suisan, data = X)
#> Df Variance F Pr(>F)
#> dist_from_suisan 1 0.01025 0.6903 0.675
#> Residual 38 0.56422河口からの距離は釣果と関係性がありそうですが、平均吹送距離や水産学部棟からの距離は、 ほとんど関係なさそうです。 とりあえず、練習として全ての変数を残したモデルを使用しようと思います。
r4 = rda(Y ~ dist_from_river + dist_from_suisan + mean_f, data = X)モデルの結果を確認します。 Constrained inertia が Unconstrained inertia より高いとき、 応答変数の散らばりは説明変数で説明できていると考えられる。 今回の解析結果を確認すると、Constrained intertia は Unconstrained inertia より とても小さいので、応答変数の散らばりは説明変数で十分説明できていません。
r4
#> Call: rda(formula = Y ~ dist_from_river +
#> dist_from_suisan + mean_f, data = X)
#>
#> Inertia Proportion Rank
#> Total 0.57446 1.00000
#> Constrained 0.06003 0.10450 3
#> Unconstrained 0.51443 0.89550 17
#> Inertia is variance
#>
#> Eigenvalues for constrained axes:
#> RDA1 RDA2 RDA3
#> 0.030020 0.021112 0.008899
#>
#> Eigenvalues for unconstrained axes:
#> PC1 PC2 PC3 PC4 PC5 PC6 PC7
#> 0.19012 0.09932 0.06286 0.03970 0.03587 0.02510 0.01805
#> PC8
#> 0.01438
#> (Showing 8 of 17 unconstrained eigenvalues)Constrained inertia はとても低かったが、勉強のために解析を進めます。 変数ごとに P 値を確認します。
anova(r4, by = "terms", permutations = 999)
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = Y ~ dist_from_river + dist_from_suisan + mean_f, data = X)
#> Df Variance F Pr(>F)
#> dist_from_river 1 0.01771 1.2393 0.274
#> dist_from_suisan 1 0.01419 0.9931 0.409
#> mean_f 1 0.02813 1.9687 0.072 .
#> Residual 36 0.51443
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1抽出される成分ごとに P 値を確認します。
anova(r4, by = "axis", permutations = 999)
#> Permutation test for rda under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = Y ~ dist_from_river + dist_from_suisan + mean_f, data = X)
#> Df Variance F Pr(>F)
#> RDA1 1 0.03002 2.1008 0.316
#> RDA2 1 0.02111 1.4774 0.409
#> RDA3 1 0.00890 0.6228 0.697
#> Residual 36 0.51443モデルの P 値を確認します。
anova(r4, permutations = 999)
#> Permutation test for rda under reduced model
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = Y ~ dist_from_river + dist_from_suisan + mean_f, data = X)
#> Df Variance F Pr(>F)
#> Model 3 0.06003 1.4003 0.137
#> Residual 36 0.51443調整済み決定係数 (Radj2) は低いですね。
RsquareAdj(r4)$r.squared
#> [1] 0.1045制約ありの序列化解析では、調整済み決定係数 \((R_{adj}^{2})\) は一般的に低くなります。
この値が高いほど、モデルの説明力が高いです。
分析結果は ggveganパッケージの fortify() 関数を使って抽出します。
rout1 = fortify(r4, axes = 1:2, scaling = 1)
rout2 = fortify(r4, axes = 1:2, scaling = 2)
calculate_equilibrium = function(X) {
# vegan scales output with a constant.
p = length(X$CA$eig)
tot = sum(X$CA$eig)
n = nrow(X$CA$u)
sqrt(2 / p) * ((n-1)*tot)^0.25
}
# biplot.
biplot1 = rout1 |> filter(str_detect(Score, "biplot")) |>
mutate(sRDA1 = 1.5*RDA1 / sqrt((RDA1^2+RDA2^2))) |>
mutate(sRDA2 = 1.5*RDA2 / sqrt((RDA1^2+RDA2^2))) |>
mutate(theta = atan(sRDA2/ sRDA1)) |>
mutate(theta = 180 * theta / pi + ifelse(RDA1 < 0, theta , theta),
hjust = ifelse(RDA1 > 0, 1, 0),
vjust = 0.5) |>
as_tibble() |>
mutate(Label = recode(Label, dist_from_river = "河口からの距離"),
Label = recode(Label, dist_from_sui = "水産学部棟からの距離"),
Label = recode(Label, mean_f = "平均フェッチ"))
biplot2 = rout2 |> filter(str_detect(Score, "biplot")) |>
mutate(sRDA1 = 2.0*RDA1 / sqrt((RDA1^2+RDA2^2))) |>
mutate(sRDA2 = 2.0*RDA2 / sqrt((RDA1^2+RDA2^2))) |>
mutate(theta = atan(sRDA2/ sRDA1)) |>
mutate(theta = 180 * theta / pi + ifelse(RDA1 < 0, theta , theta),
hjust = ifelse(RDA1 > 0, 1, 0),
vjust = 0.5) |>
as_tibble() |>
mutate(Label = recode(Label, dist_from_river = "河口からの距離"),
Label = recode(Label, dist_from_sui = "水産学部棟からの距離"),
Label = recode(Label, mean_f = "平均フェッチ"))
# サイト.
sites1 = rout1 |>
filter(str_detect(Score, "sites")) |>
bind_cols(X) |>
as_tibble()
sites2 = rout2 |>
filter(str_detect(Score, "sites")) |>
bind_cols(X) |>
as_tibble()
# 生物種.
species1 = rout1 |>
filter(str_detect(Score, "species"))
species2 = rout2 |>
filter(str_detect(Score, "species"))分析の結果を可視化します。 説明変数から合成変量が構成され、それが応答変数の分散を説明する割合は最大化されています。
# 表示したい生物種.
SP_LABEL = c("アオリイカ", "シロギス", "ブリ", "スズキ",
"タチウオ", "イイダコ", "メバル", "カサゴ",
"メジナ", "マダイ", "クロダイ", "マアジ")
XLABEL = "RDA[1]"
YLABEL = "RDA[2]"
# scaling 1.
# 作図.
p1 = ggplot() +
geom_vline(xintercept = 0, linetype = "dashed", color = "grey50") +
geom_hline(yintercept = 0, linetype = "dashed", color = "grey50") +
ggforce::geom_circle(aes(x0 = 0, y0 = 0, r = 0), color = "grey50") +
# geom_point(aes(x = RDA1, y = RDA2, color = size_scl_mean),
# data = sites1, size = 5) +
# 生物種.
geom_text_repel(aes(x = RDA1, y = RDA2, label = Label),
verbose = T, force = 1, box.padding = 0, point.padding = 0,
data = species1 |> filter(Label %in% SP_LABEL), size = 3, color = "red") +
# 矢印
geom_segment(aes(x = 0, y = 0, xend = 2*RDA1, yend = 2*RDA2),
data = biplot1,
arrow = arrow(20, unit(2, "mm"), type = "closed"),
color = "black", size = 1) +
# 矢印の延長線.
geom_segment(aes(x = 0, y = 0, xend = sRDA1, yend = sRDA2),
alpha = 0.25, size = 7, data = biplot1, color = "gray70") +
geom_segment(aes(x = 0, y = 0, xend = -sRDA1, yend = -sRDA2),
alpha = 0.25, size = 7, data = biplot1, color = "gray70") +
# 説明変数の文字.
geom_text(aes(x = sRDA1, y = sRDA2, label = Label, angle = theta, hjust = hjust, vjust = vjust),
data = biplot1, size = 3, color = "black") +
# サイト.
# geom_label_repel(aes(x = RDA1, y = RDA2, label = spot),
# verbose = T, force = 1, box.padding = 0, point.padding = 0,
# data = sites1, size = 3) +
scale_color_viridis_c(begin = 0.1, end = 0.8, option = "B") +
scale_x_continuous(parse(text = XLABEL), limits = c(-2,2)) +
scale_y_continuous(parse(text = YLABEL), limits = c(-2,2)) +
coord_equal() +
labs(title = "Distance biplot (scaling = 1)") +
theme(legend.position = "none")
# scaling 2.
p2 = ggplot() +
geom_vline(xintercept = 0, linetype = "dashed", color = "grey50") +
geom_hline(yintercept = 0, linetype = "dashed", color = "grey50") +
geom_point(aes(x = RDA1, y = RDA2, color = n), data = sites2, size = 3) +
# 矢印
geom_segment(aes(x = 0, y = 0, xend = RDA1, yend = RDA2),
data = biplot2,
arrow = arrow(20, unit(2, "mm"), type = "closed"),
color = "black", size = 1) +
# 矢印の延長線.
geom_segment(aes(x = 0, y = 0, xend = sRDA1, yend = sRDA2),
alpha = 0.25, size = 7, data = biplot2, color = "gray70") +
geom_segment(aes(x = 0, y = 0, xend = -sRDA1, yend = -sRDA2),
alpha = 0.25, size = 7, data = biplot2, color = "gray70") +
# 説明変数の文字.
geom_text(aes(x = sRDA1, y = sRDA2, label = Label, angle = theta, hjust = hjust, vjust = vjust),
data = biplot2, size = 2, color = "black") +
# サイト.
# geom_text_repel(aes(x = RDA1, y = RDA2, label = spot),
# verbose = T, force = 1, box.padding = 0, point.padding = 0,
# data = sites2, size = 3, color = "steelblue4") +
# # 生物種.
# geom_text_repel(aes(x = RDA1, y = RDA2, label = Label),
# verbose = T, force = 1, box.padding = 0, point.padding = 0,
# data = species2 |> filter(Label %in% SP_LABEL), size = 3, color = "dodgerblue4") +
scale_color_viridis_c(end = 0.9, option = "B",
guide = guide_colorbar(title = "種数",
title.position = "top", title.hjust = 0.5,
ticks = F, label = T)) +
scale_x_continuous(parse(text = XLABEL), limits = c(-2, 2)) +
scale_y_continuous(parse(text = YLABEL), limits = c(-2, 2)) +
coord_equal() +
labs(title = "Distance biplot (scaling = 2)")
p1 + p2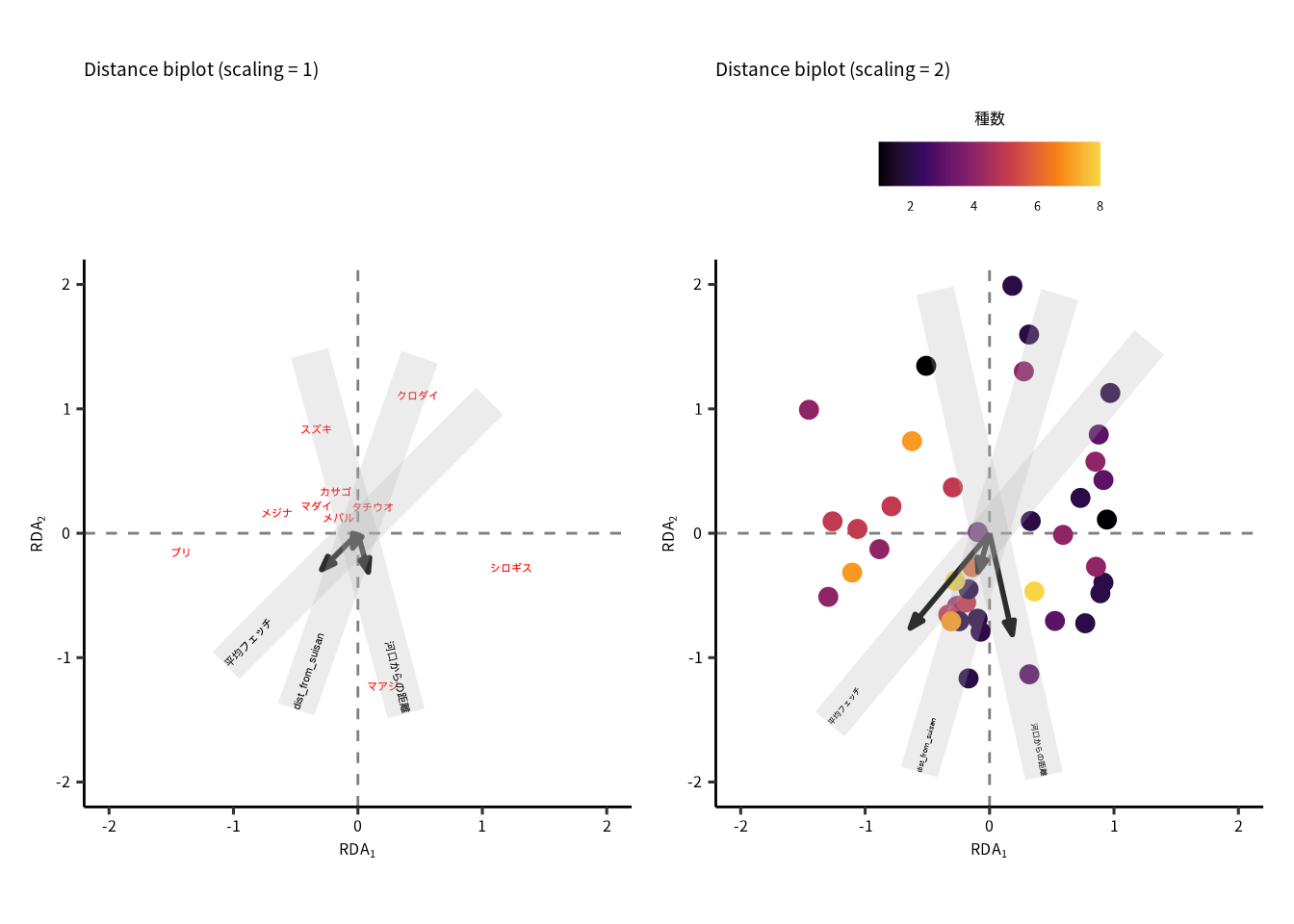
Figure 15.1: 冗長性解析の結果は 2 種類の図で確認できます。 矢印の起点はその変数の平均値を表しています。 矢印の反対方向は、変数値が変数平均値より低い方向を示しています。 矢印が向かく方法は変数値が増加している方向を示しています。 (右)scaling 1 では, 類似度が地点間の距離として表現されています。近いものは似ていて、離れているものは似ていていない。マアジとクロダイは全く反対側に位置するので、釣れた場所の違いが原因かもしれないです。 (左)scaling 2 では, 相関関係が地点間の角度として表現されています。起点から点まで矢印を伸ばした場合、矢印間の角が鈍角のとき、負の相関関係を示していて、鋭角のときは正の相関関係を示しています。 生物群集と環境要因のかかわりを平面に落とし込むことが出来ました。
#> text repel complete in 144 iterations (0.00s), 2 overlaps