一元配置分散分析

Comparing multiple groups with ANOVA

Note

解析の紹介に使った疑似データは次のようにつくりました。

set.seed(2021) # 疑似乱数のシードを設定する
nA = 6         # サンプル数を決める
nB = 6
nC = 6
meanA = 20     # 真の平均値
meanB = 22
meanC = 18
sigmaA = 1     # 真の標準偏差
sigmaB = 1
sigmaC = 1
siteA = rnorm(nA, meanA, sigmaA) |> round(1) # データを発生する
siteB = rnorm(nB, meanB, sigmaB) |> round(1)
siteC = rnorm(nC, meanC, sigmaC) |> round(1)

# tibble を組み立てる
dset = tibble(g = c("A", "B", "C"), data = list(siteA, siteB, siteC)) |> 
  unnest(data) |> 
  mutate(g = factor(g))

ノコギリモク (Sargassum macrocarpum) の疑似データ

Table 1: Size (mm) of juvenile Sargassum macrocarpum（ノコギリモク）.

Sample	Site A	Site B	Site C
1	19.9	22.3	18.2
2	20.6	22.9	19.5
3	20.3	22.0	19.6
4	20.4	23.7	16.2
5	20.9	20.9	19.6
6	18.1	21.7	18.1

Note

ノコギモクの大きさは Table 1 に示しています。サンプルは 3 箇所（3群）から採取しました。各サンプルに個体数番号もふっています。

データは上のノートに紹介したコードで発生しました。

データの可視化

ggplot(dset) + 
  geom_point(aes(x = g, y = data, color = g),
             size = 2,
             position = position_jitter(0.1)) +
  scale_color_manual("", values = viridis::viridis(4)) +
  labs(y = "Width (mm)", x = "Site") +
  theme(legend.position = "top")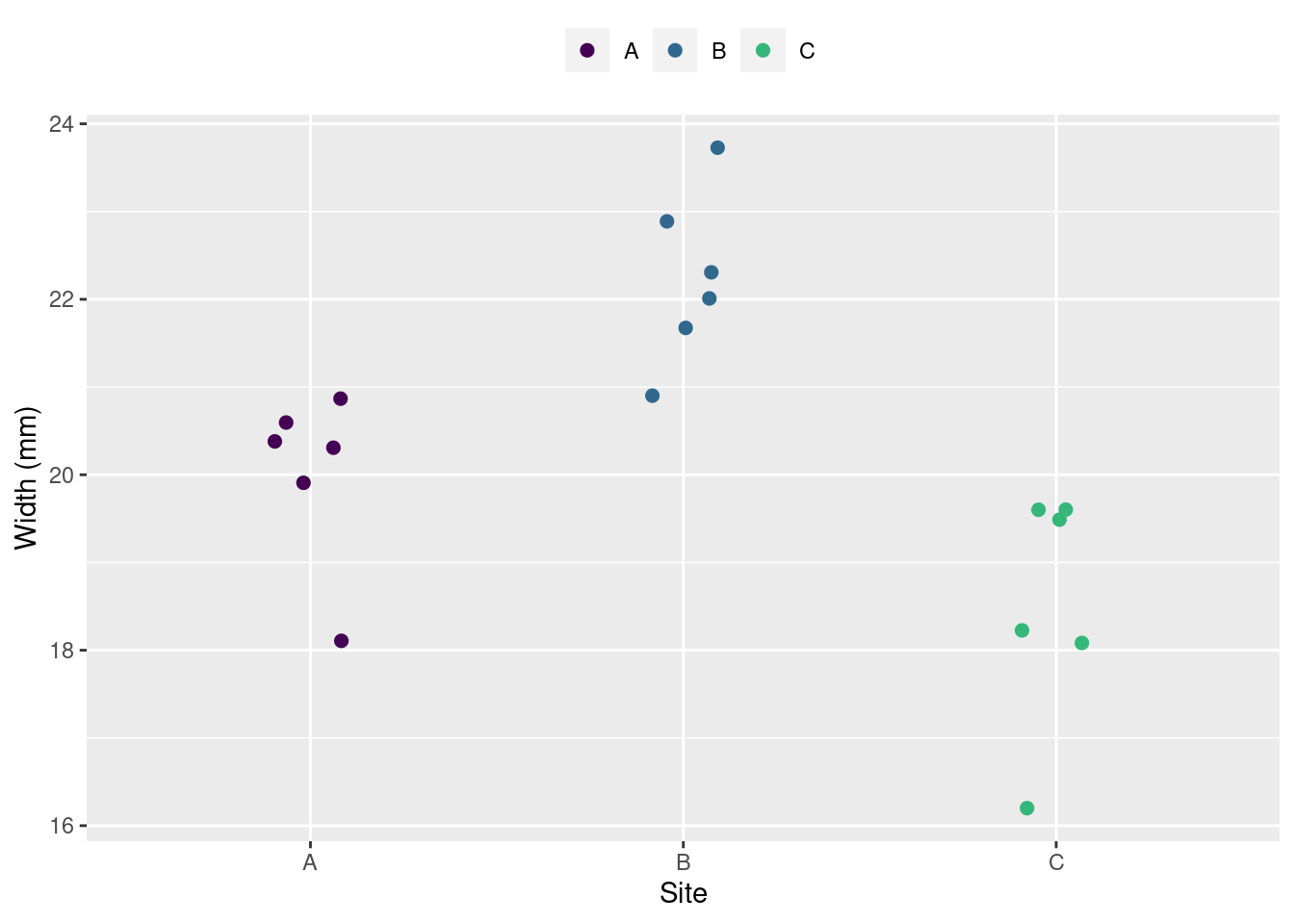

各サイトの平均値 (\overline{x}), 標準偏差 (s), と標準誤差 (s.e.) は、

\overline{x}_A= 20; s_A= 1; s.e. = 0.41
\overline{x}_B= 22.2; s_B= 0.97; s.e. = 0.4
\overline{x}_C= 18.5; s_C= 1.34; s.e. = 0.55

仮説を決める

Important

解析する前に作業仮説、帰無仮説、対立仮説を設定する必要があります。

Working hypothesis

作業仮設: ノコギリモクの大きさは採取した場所によって異なる。

記述統計量によって、平均値以外の統計量（標準偏差と標準誤差）は似ています。
\overline{x}_A= 20; s= 1; s.e. = 0.41
\overline{x}_B= 22.2; s= 0.97; s.e. = 0.4
\overline{x}_C= 18.5; s= 1.34; s.e. = 0.55

帰無仮説と対立仮説

統計学的に解析するための帰無仮説と対立仮説を決めます。

H_0 (null hypothesis 帰無仮説・ヌル仮説): ノコギリモクの大きさは場所によって異ならない
H_A (alternative hypothesis 対立仮設): ノコギリモクの大きさは場所によって異なる

ナイーブなペア毎の t 検定

とりあえず、場所のペア毎の t 検定を実施します。このとき、3 つの帰無仮説が必要なので、(hypothesis?) と違います。

H_0,A-B: Site A と Site B の大きさは同じ
H_0,A-C: Site A と Site C の大きさは同じ
H_0,B-C: Site B と Site C の大きさは同じ

では、それぞれの t 検定を実施します。

Site A and B の t 検定

resultAB = dset |> filter(!str_detect(g, "C"))
resultAB = t.test(data ~ g, data = resultAB)
resultAB


    Welch Two Sample t-test

data:  data by g
t = -3.8886, df = 9.9893, p-value = 0.003022
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
 -3.486976 -0.946357
sample estimates:
mean in group A mean in group B 
       20.03333        22.25000

t値は -3.889、P値は 0.003 です。 0.003 \le 0.05 なので、帰無仮説は棄却できます。

Site A and C の t 検定

resultAC = dset |> filter(!str_detect(g, "B"))
resultAC = t.test(data ~ g, data = resultAC)
resultAC


    Welch Two Sample t-test

data:  data by g
t = 2.1968, df = 9.2717, p-value = 0.05477
alternative hypothesis: true difference in means between group A and group C is not equal to 0
95 percent confidence interval:
 -0.03773888  3.03773888
sample estimates:
mean in group A mean in group C 
       20.03333        18.53333

t値は 2.197、P値は 0.0548 です。 0.0548 \ge 0.05 なので、帰無仮説は棄却できません。

Site B and C の t 検定

resultBC = dset |> filter(!str_detect(g, "A"))
resultBC = t.test(data ~ g, data = resultBC)
resultBC


    Welch Two Sample t-test

data:  data by g
t = 5.5063, df = 9.1228, p-value = 0.0003595
alternative hypothesis: true difference in means between group B and group C is not equal to 0
95 percent confidence interval:
 2.192862 5.240472
sample estimates:
mean in group B mean in group C 
       22.25000        18.53333

t値は 5.506、P値は 0.0004 です。 0.0004 \le 0.05 なので、帰無仮説は棄却できます。

t検定の結果をまとめました。

Table 2: Summary of three t-tests.

Pair	Difference	t-value	P-value	d.f.	95% CI	Is P ≤ 0.05?
B-A	-2.216667	-3.888623	0.0030224	9.989348	-3.487 to -0.95	Yes
C-A	1.500000	2.196821	0.0547748	9.271711	-0.038 to 3.04	No
C-B	3.716667	5.506257	0.0003595	9.122821	2.193 to 5.24	Yes

d.f. は Welch-Satterthwaite 式で求めた自由度¹、95% CI は 95% 信頼区間です。

¹ degrees-of-freedom

第１種の誤り (accepting a false H₀)

第１種の誤り

H₀ が FALSE のときに帰無仮説を棄却できなかった誤りです。

t 検定を 1 回実施したときの誤りは

\text{Type I error rate} = \alpha = 0.05

t 検定を 2 回実施したときの誤りは

1 - (1 - \alpha) \times (1 - \alpha) = 1 - (1-\alpha)^2=0.0975

t 検定を 3 回実施したときの誤りは

1 - (1 - \alpha) \times (1 - \alpha) \times (1 - \alpha)= 1 - (1-\alpha)^3=0.142625

t 検定を h 回実施したとき、第１種の誤りは 1 - (1-\alpha)^h です。

群が増えると大変なことなる

n 群のサンプルの全ペア毎の比較がしたい場合、 h のペア (k = 2) が存在します。

h = \binom{n}{k}=\frac{n!}{k!(n-k!)}

ペア毎の h の数を求める式は次のようになります。

h = \binom{n}{2}=\frac{n!}{2!(n-2!)} = \frac{n(n-1)}{2}

例えば、5 site の場合、10 のペアが存在します。ペア毎の t 検定をしたら、第１種の誤りは

1 - (1-0.05)^{10}=0.4012631

R での求め方

alpha = 0.05       # 有意水準
k = 2              # ペアだから 2
n = 5              # 比較する群・場所・グループの数
h = choose(n, k)   # ペアの数
1 - (1 - alpha)^h  # 第１種の誤り

[1] 0.4012631

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.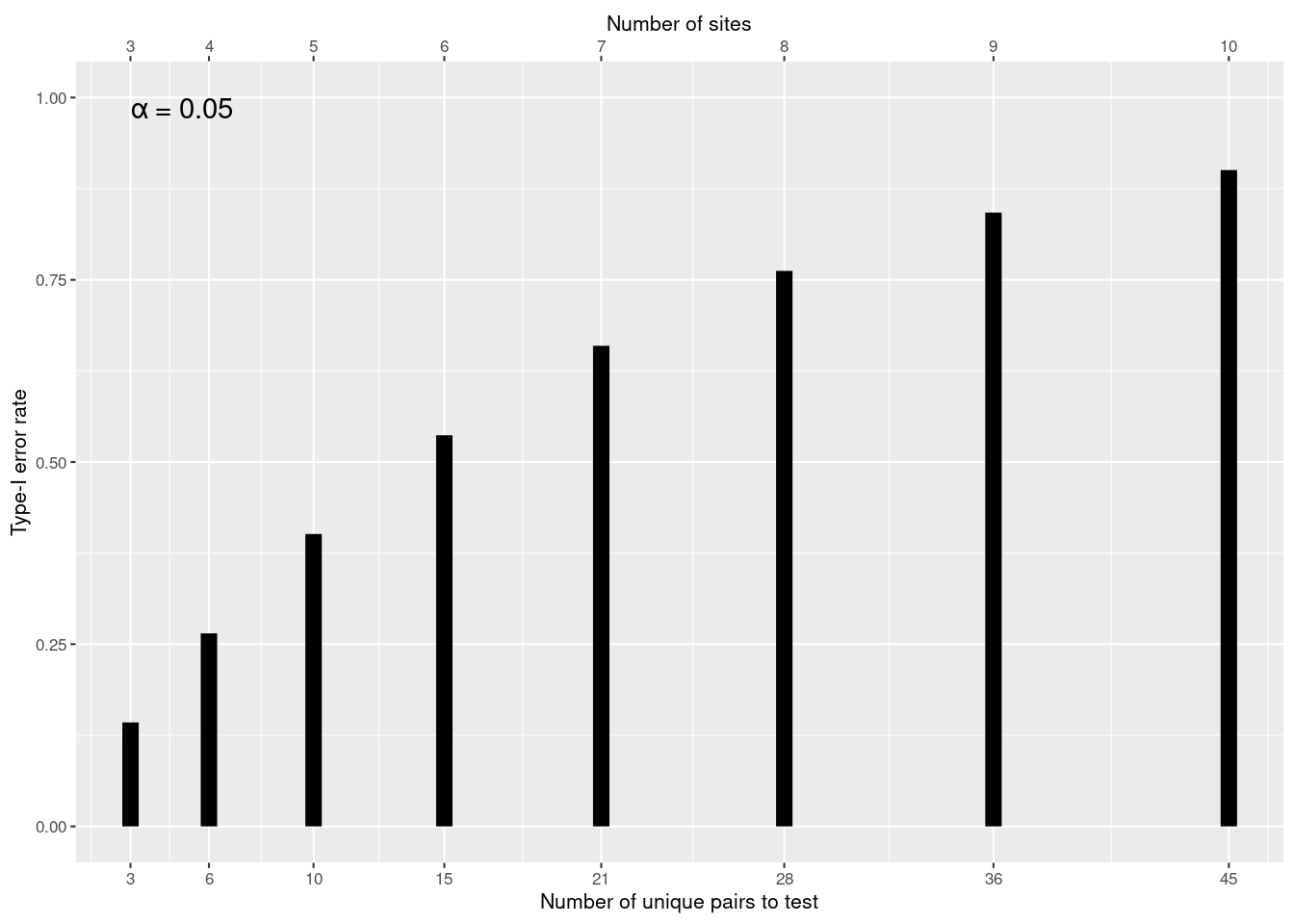

比較する群が増えると、t 検定を繰り返して実施すると、第１種の誤りを起こしやすい。

一元配置分散分析

One-Way ANOVA (一元配置分散分析)

複数群（因子の水準）の解析は 一元配置分散分析)² 用います。

² One-Way ANOVA (One-Way Analysis of Variance

因子・要因³：説明変数、一般的には離散型な変数
水準⁴：説明変数における値、レベル、要素

³ factor

⁴ level, factor level

分散分析の帰無仮説は、

\mu_1 = \mu_2 = \cdots = \mu_i

つまり、一つの検定で複数群の平均値を同時に解析するから、第１種の誤りは 0.05 に抑えられる。

分散分析のモデル式は次のように表せます。

x_{ij} = \mu_i + \epsilon_{ij}

水準 i とサンプル j の値は x_{ij}です。水準 i の平均値は \mu_i です。モデルの残渣^{[residual]または誤差項}[error term]は \epsilon_{ij} です。

一元配置分散分析表

Factor	Degrees-of-freedom (df)	Sum-of-Squares (SS)	Mean-square (MS)	F-value	P-value
A	$df_A = I-1$	$SS_A$	$MS_A = SS_A / df_A$	$MS_A / MS_R$	$qf(1-α, df_A, df_R)$
e	$df_R = I(J-1)$	$SS_R$	$MS_R = SS_R / df_R$
	$df_T =IJ-1$	$SS_T$

因子は A⁵
残渣は e⁶
水準数は I⁷
サンプル数は　J⁸
水準間平方和は SS_A⁹
残渣平方和は SS_R¹⁰
総平方和は SS_T¹¹
水準間平均平方は MS_A¹²
残渣平均平方は MS_R¹³
F値¹⁴は MS の比です。

⁵ factor

⁶ residual

⁷ number of levels

⁸ number of samples

⁹ among levels sum-of-squares (SS)

¹⁰ residual SS

¹¹ total SS

¹² among levels mean square (MS)

¹³ residual mean square (MS)

¹⁴ F-value

平方和の方程式

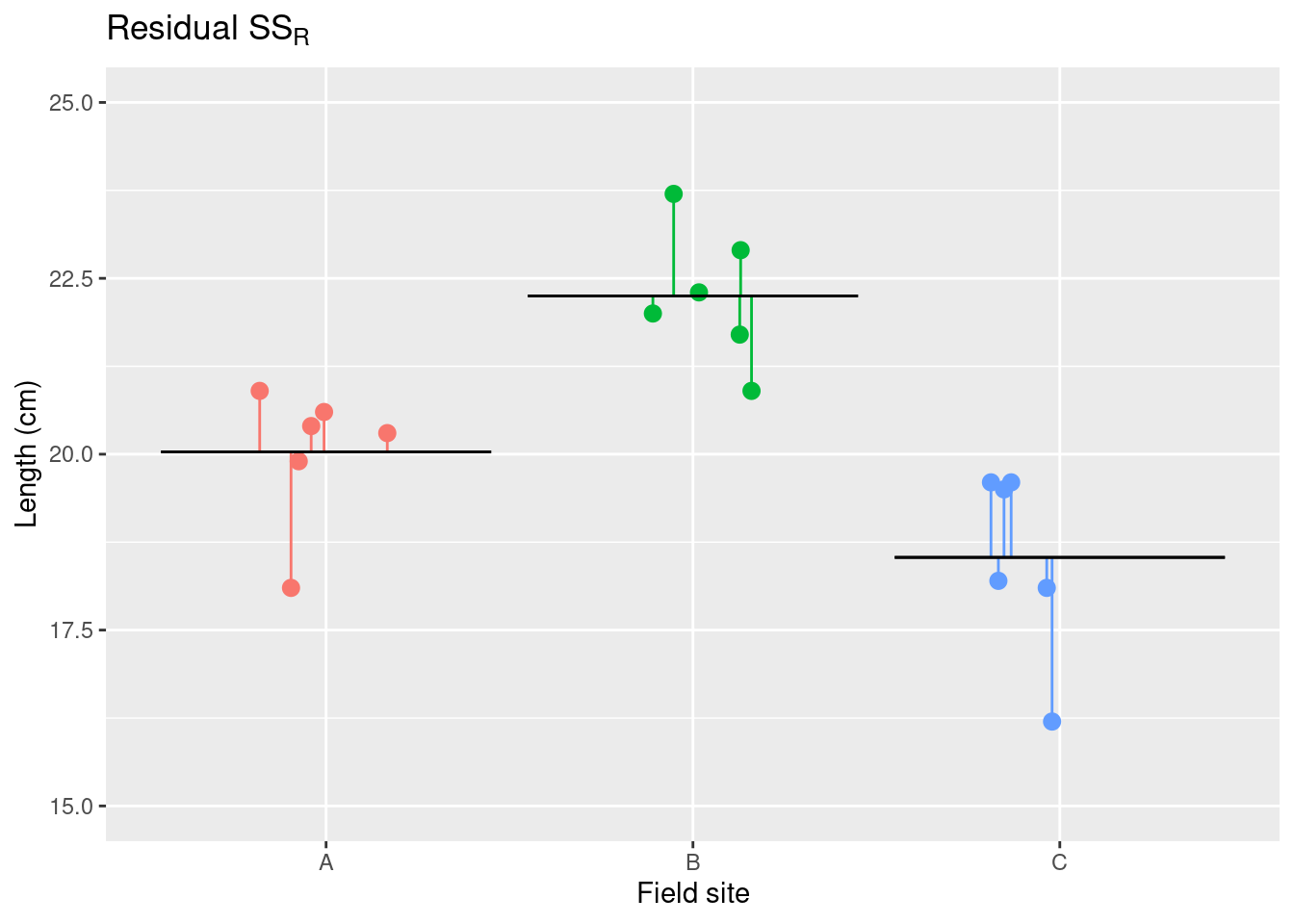
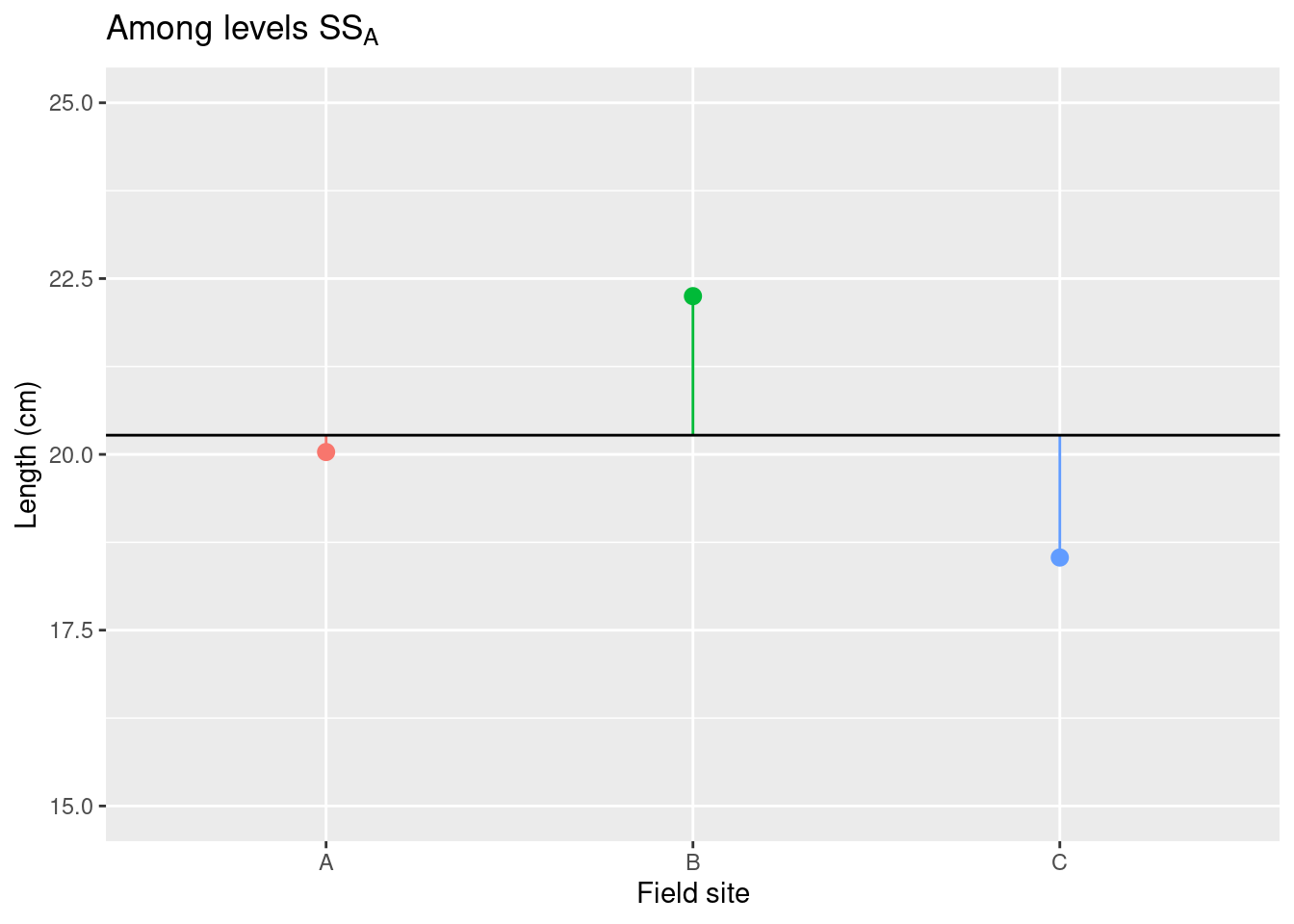
\underbrace{\sum_{i=1}^I\sum_{j=1}^J(x_{ij} - \overline{\overline{x}})^2 }_{\text{総平方和}\;(SS_T)} = \overbrace{J\sum_{i=1}^I(\overline{x}_{i}-\overline{\overline{x}})^2}^{\text{水準間平方和}\;SS_A} + \underbrace{\sum_{i=1}^I\sum_{j=1}^J(x_{ij} - \overline{x}_i)^2}_{\text{残渣平方和}\;SS_R}

標本平均は \bar{x}_i、総平均は \bar{\bar{x}} です。

Decomposing the sum-of-squares

残渣平方和：各サンプルの値は点、グループ毎の平均値は黒線で示しています。黒線から点の縦線は残渣を表しています。

水準間平方和：各グループの平均値は点、総平均は黒線で示しています。黒線から点の縦線はグループ毎の平均値と総平均の違いを表しています。

分散分析の統計量

F = \left . \frac{SS_A}{I-1} \right / \frac{SS_R}{I(J-1)} = \frac{SS_A}{SS_R} \frac{I(J-1)}{I-1} = \frac{MS_A}{MS_R}

F値は自由度 \text{df}_1 = I-1, \text{df}_2 = I(J-1) のF分布に従います。水準の数は I、水準ごとのサンプルの数は J です。

Note

F値の分子¹⁵ が大きとき、または分母¹⁶が小さいとき、F値は大きいです。
F値とP値は反比例します。

¹⁶ denominator

¹⁵ numerator

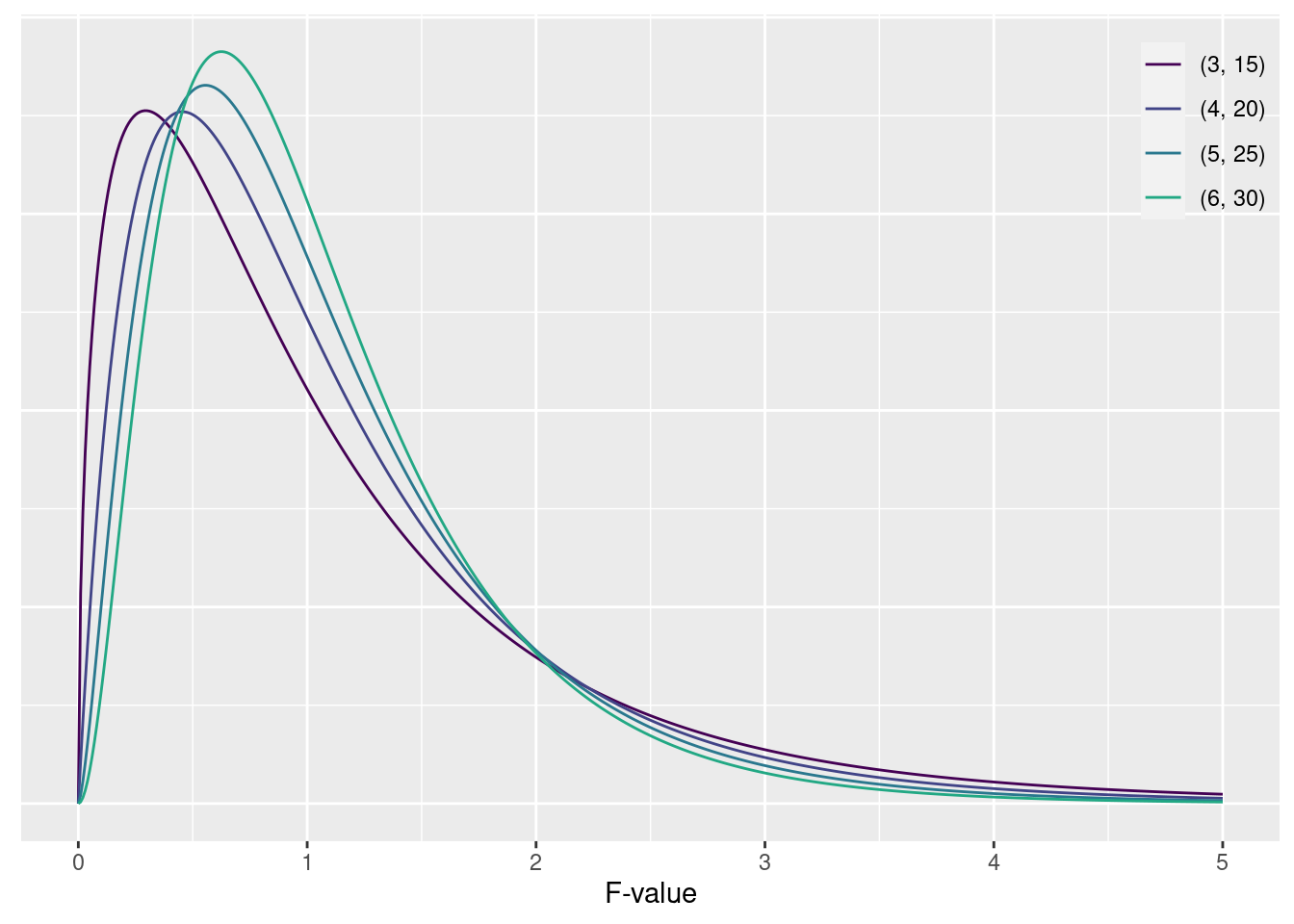
F値の確率密度関数

P(x|\text{df}_1, \text{df}_2) = \frac{1}{\mathrm{B}\left(\frac{\text{df}_1}{2}, \frac{\text{df}_2}{2}\right)}\left(\frac{\text{df}_1}{\text{df}_2}\right)^{\left(\frac{\text{df}_1}{2}\right)}x^{\left(\frac{\text{df}_1}{2}-1\right)}\left(1+\frac{\text{df}_1}{\text{df}_2}x\right)^{\left(-\frac{\text{df}_1+\text{df}_2}{2}\right)} \mathrm{B}(\text{df}_1, \text{df}_2)=\int_0^1t^{x-1}(1-t)^{y-1}dt はベータ関数¹⁷ といいます。 \text{df}_1 と \text{df}_2 は自由度、x は確率変数です。

¹⁷ Beta function

一元配置分散分析表の仮定

分散分析するときに注意する仮定

水準毎の母分散は等しい
残渣は正規分布に従う
観測値はお互いに独立であり、同一分布に従う
観測変数は連続変数¹⁸
説明変数は離散変数¹⁹

¹⁸ continuous

¹⁹ discrete

Rにおける解析

解析例に使うデータは thedata.csv に保存したので、まずは読み込みます。

# Read data from a csv file
dset = read_csv("thedata.csv")

データをグループ化したあと、最初の 2 行を表示する。

dset |> group_by(site) |> slice(1:2)

# A tibble: 6 × 2
# Groups:   site [3]
  site    obs
  <fct> <dbl>
1 A      19.9
2 A      20.6
3 B      22.3
4 B      22.9
5 C      18.2
6 C      19.5

帰無仮説を当てはめる。

nullmodel = lm(obs ~ 1, data = dset) # 帰無モデル、ヌルモデル

フルモデル（対立仮説）を当てはめる。

fullmodel = lm(obs ~ site, data = dset) # 対立モデル、フルモデル

分散分析の結果

帰無仮説と対立仮説のモデル結果を用いた方法。

anova(nullmodel, fullmodel, test = "F")

Analysis of Variance Table

Model 1: obs ~ 1
Model 2: obs ~ site
  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1     17 60.656                                  
2     15 18.702  2    41.954 16.825 0.0001471 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

F値は 16.825、自由度は df₁ = 2 と df₂ = 15 です。よって、P値は 0.000147 です。有意水準が \alpha = 0.05 、自由度が　(2, 15) のときのF値は 3.682.

フルモデルの結果でけ用いた解析

anova(fullmodel)

Analysis of Variance Table

Response: obs
          Df Sum Sq Mean Sq F value    Pr(>F)    
site       2 41.954 20.9772  16.825 0.0001471 ***
Residuals 15 18.702  1.2468                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

aov() 関数を用いた方法

このとき、lm() は不要です。

aovout = aov(obs ~ site, data = dset)
summary(aovout)

            Df Sum Sq Mean Sq F value   Pr(>F)    
site         2  41.95  20.977   16.82 0.000147 ***
Residuals   15  18.70   1.247                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Important

分散分析の帰無仮説は \mu_0 = \mu_1 = \cdots \mu_i なので、ペア間の検定ではないです。

多重比較²⁰

多重比較

分散分析の帰無仮説を棄却したら、ペア毎の比較がしたくなります。第１種の誤りを抑える多重比較の検定は豊富に存在します。

Bonferroni Procedure (ボンフェロニ法)
Holm-Bonferroni Method (ホルム = ボンフェロニ法)
Tukey’s Honest Signiﬁcant Difference Test (テューキーの HSD 検定)
Tukey-Kramer method, Tukey’s test
Scheffe’s Method (シェッフェの方法)
Dunnett’s Test (ダネットの検定)
Fisher’s Least Signiﬁcant Difference (フィッシャーの最小有意差法)
Duncan’s new multiple range test (ダンカンの新多重範囲検定)

1 から 4 はペア毎の比較です。ダネットの検定は水準に対する比較です。フィッシャーとダンカンの検定の第１種の誤りは高いので、使用しないでください。

多重比較用 R パッケージ

多重比較用の関数は次のパッケージにあります。

multcomp
emmeans

ここでは、emmeans を紹介します。

library(emmeans) # 多重比較用パッケージ
library(nlme)    # gls() 関数はこのパッケージにある


Attaching package: 'nlme'

The following object is masked from 'package:dplyr':

    collapse

繰り返しウェルチの t 検定

説明のために紹介しています。実際の解析には使わないでください。

glsmodel = gls(obs ~ site, data = dset, 
               weights = varIdent(form = ~ 1|site))
emout = emmeans(glsmodel, specs = pairwise ~ site, adjust = "none")
emout$contrasts |> summary(infer =T)

 contrast estimate    SE   df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.570 9.99  -3.4870   -0.946  -3.889  0.0030
 A - C        1.50 0.683 9.26  -0.0381    3.038   2.197  0.0548
 B - C        3.72 0.675 9.11   2.1925    5.241   5.506  0.0004

Degrees-of-freedom method: satterthwaite 
Confidence level used: 0.95

第１種の誤りを調整していません。

繰り返し t 検定

説明のために紹介しています。実際の解析には使わないでください。

emout = emmeans(fullmodel, specs = pairwise ~ site, data = dset, adjust = "none")
emout$contrasts |> summary(infer =T)

 contrast estimate    SE df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.645 15   -3.591   -0.843  -3.438  0.0037
 A - C        1.50 0.645 15    0.126    2.874   2.327  0.0344
 B - C        3.72 0.645 15    2.343    5.091   5.765  <.0001

Confidence level used: 0.95

第１種の誤りを調整していません。

ボンフェロニ法

emout = emmeans(fullmodel, specs = pairwise ~ site, data=dset, adjust = "bonferroni")
emout$contrasts |> summary(infer =T)

 contrast estimate    SE df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.645 15   -3.953    -0.48  -3.438  0.0110
 A - C        1.50 0.645 15   -0.237     3.24   2.327  0.1032
 B - C        3.72 0.645 15    1.980     5.45   5.765  0.0001

Confidence level used: 0.95 
Conf-level adjustment: bonferroni method for 3 estimates 
P value adjustment: bonferroni method for 3 tests

P値は p_{adj} =m\times p によって求められました.

ホルム=ボンフェロニ法

emout = emmeans(fullmodel, specs = pairwise ~ site, data=dset, adjust = "holm")
emout$contrasts |> summary(infer =T)

 contrast estimate    SE df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.645 15   -3.953    -0.48  -3.438  0.0073
 A - C        1.50 0.645 15   -0.237     3.24   2.327  0.0344
 B - C        3.72 0.645 15    1.980     5.45   5.765  0.0001

Confidence level used: 0.95 
Conf-level adjustment: bonferroni method for 3 estimates 
P value adjustment: holm method for 3 tests

P値は低い値から高い値へ並べ替えてから、p_{adj} = (m+1-k)\times p によって求めます。 m は比較の数、 k は比較の指数です。

Note

ボンフェロニ法とホルム=ボンフェロニ法の P値は次のように求められます。

emout = emmeans(fullmodel, specs = pairwise ~ site, adjust = "none")
x = emout$contrasts  |>  as_tibble()
x  |>  arrange(p.value)  |> 
  mutate(k = 1:3)  |> mutate(m = n())  |> 
  mutate(p.bonferroni = p.value * m,
         p.holm = p.value * (m + 1 - k))  |> 
  select(contrast, m, k, starts_with("p"))

# A tibble: 3 × 6
  contrast     m     k   p.value p.bonferroni   p.holm
  <chr>    <int> <int>     <dbl>        <dbl>    <dbl>
1 B - C        3     1 0.0000373     0.000112 0.000112
2 A - B        3     2 0.00366       0.0110   0.00731 
3 A - C        3     3 0.0344        0.103    0.0344

テューキーのHSD法

emout = emmeans(fullmodel, specs = pairwise ~ site, data=dset, adjust = "tukey")
emout$contrasts |> summary(infer =T)

 contrast estimate    SE df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.645 15   -3.891   -0.542  -3.438  0.0096
 A - C        1.50 0.645 15   -0.174    3.174   2.327  0.0826
 B - C        3.72 0.645 15    2.042    5.391   5.765  0.0001

Confidence level used: 0.95 
Conf-level adjustment: tukey method for comparing a family of 3 estimates 
P value adjustment: tukey method for comparing a family of 3 estimates

P値はステュデント化範囲の分布²¹に従います。

²¹ Studentized range distribution

シェッフェの方法

emout = emmeans(fullmodel, specs = pairwise ~ site, data=dset, adjust = "scheffe")
emout$contrasts |> summary(infer =T)

 contrast estimate    SE df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.645 15   -3.966   -0.467  -3.438  0.0128
 A - C        1.50 0.645 15   -0.249    3.249   2.327  0.0991
 B - C        3.72 0.645 15    1.967    5.466   5.765  0.0002

Confidence level used: 0.95 
Conf-level adjustment: scheffe method with rank 2 
P value adjustment: scheffe method with rank 2

P値はF分布に従います。

ダネットの検定

emout = emmeans(fullmodel, specs = trt.vs.ctrl ~ site, ref = 2)
emout$contrasts |> summary(infer =T)

 contrast estimate    SE df lower.CL upper.CL t.ratio p.value
 A - B       -2.22 0.645 15     -3.8   -0.633  -3.438  0.0070
 C - B       -3.72 0.645 15     -5.3   -2.133  -5.765  0.0001

Confidence level used: 0.95 
Conf-level adjustment: dunnettx method for 2 estimates 
P value adjustment: dunnettx method for 2 tests

ダネットの検定は、各水準は標準水準と比較する方法です。 P値は多変量 t 分布に従います。

多重比較のおすすめ

比較: A – B, A – C, B – C テューキーのHSD法
比較: A – B, A – C, A – D ダネット法

²⁰ multiple comparisons

ノコギリモク (Sargassum macrocarpum) の疑似データ

データの可視化

仮説を決める

帰無仮説と対立仮説

ナイーブな ペア毎の t 検定

Site A and B の t 検定

Site A and C の t 検定

Site B and C の t 検定

第１種の誤り (accepting a false H0)

群が増えると大変なことなる

一元配置分散分析

One-Way ANOVA (一元配置分散分析)

一元配置分散分析表

平方和の方程式

Decomposing the sum-of-squares

分散分析の統計量

F値の確率密度関数

一元配置分散分析表の仮定

Rにおける解析

分散分析の結果

多重比較20

多重比較

多重比較用 R パッケージ

繰り返しウェルチの t 検定

繰り返し t 検定

ボンフェロニ法

ホルム=ボンフェロニ法

テューキーのHSD法

シェッフェの方法

ダネットの検定

多重比較のおすすめ

ナイーブなペア毎の t 検定

第１種の誤り (accepting a false H₀)

多重比較²⁰